2023-06-19

「AWS上にマラソンマッチ用のジャッジ環境を作った」をChatGPTに投げて、Lambdaを使ったAHC用のジャッジ環境を作る。

概要
ChatGPTのいいなりになればOK
はまったところ
最後にChatGPTによるブログ

概要

Webやサーバー関係に詳しくなくても、良い記事をChatGPTに投げればなんとかなる。

ChatGPTのいいなりになればOK

AtCoder Heuristics Contest（AHC）用にAWS Lambdaを使った自作ジャッジを作りたいなと思っていたので重い腰を上げましたがその辺の知識はありません。そこでyunixさんの素晴らしい記事を発見します。
yunix-kyopro.hatenablog.com

AWSを触ったことがない人向けには書いていないです。すいません...

と書いてありますが、気にせず上記の記事をコピペしてChatGPTに丸投げします。

以下のようにコマンドつきで基本的な部分から手取り足取り教えてくれます。

Ubuntuでも出来ますか？レベルの質問でもChatGPTは丁寧に回答してくれます。

あとは、「エラーが出たら、エラーログを添付して質問」「ハマったら原因を適当に推測してもらう」を繰り返すと、自分用のジャッジが作れます。詳しく勉強したい部分があったらそれも質問するといいです。

以下が実行結果です。できました。yunixさんありがとうございます。

はまったところ

typescriptを使った設定にする必要があった。

CDK（AWS Cloud Development Kit ）はpythonやtypescriptで設定できますが、記事に載っていたのはtypescriptだったので質問しなおしました。

リージョン間違いでログが何も見れなかった…

エラーログやLambdaの各種情報は何も設定しなくても表示されます。出てなければ何かおかしいです。この手の問題があると何が起こっているかさっぱり分からないので最初に直しましょう。ChatGPTはひどい勘違い系も割とヒントをくれるのが良いです。

ログを見る場合はhttps://console.aws.amazon.comにCloudWatchを追加すると見れます。python内でprintで標準出力したものもここで見れます。特別な設定はいりませんがリージョンを間違えていると何も見れません。

ジャッジ環境のディレクトリ構成が分からなかった。

記事に載っている1つ目のtypescriptはlib以下に置きます。

記事に載っている2つ目のDockerfile, 3つ目のhandlers.pyはlambda以下に置きます。また、requirements.txt（空ファイルで良い）も置く必要があります。

なお、main.cppやAHCのテスターを置くコンテスト毎のディレクトリとは別のものです。記事に載っている4つ目のpythonスクリプトは、コンテスト毎のディレクトリからmain.cppをS3に送ったりするのに使います。

別なバケット名を設定していた。

元の記事のpython実行スクリプトが以下のようになっているので、"バケット名"を書く必要があります。

バケットは２つ出来ているかもしれませんが、marathonjudge～のほうを設定します。もう一方のcdk-～はAWS CDKが、AWS CDK自体が管理するためのバケットの名前です

各種パスの更新をわすれていた

handlers.pyを実行したら、cdk deployコマンドでデプロイしなおすのも忘れないでください。

# handlers.py
import os
import json

import boto3


def entry_handler(event, context):
    timestamp = event["timestamp"]
    contest_name = event["contest_name"]
    N = 50
    result = [
       {
            "test_path": f"{contest_name}/in/{i:04}.txt",  # 要変更。テスト用入力ファイルのパス
            "timestamp": timestamp, 
            "contest": contest_name, 
            "id": f"{i:04}"
       } 
       for i in range(0, N, 1)
    ]
    return {"tasks": result}


def exec_handler(event, context):
    print(event, os.environ["s3Bucket"])
    # 前の段からテストファイルのパス・コンテスト名を取得
    test_path = event["test_path"]
    contest_name = event["contest"]
    test_id = event["id"]
    timestamp = event["timestamp"]

    # ソースコードを取得してビルドする
    bucket = boto3.resource("s3").Bucket(os.environ["s3Bucket"])
    bucket.download_file(f"{contest_name}/main.cpp", "/tmp/main.cpp") # {contest_name}/main.cpp。ここは記事に載っている4つめのスクリプトを使えばこのままで良い。
    os.system("g++ -O2 /tmp/main.cpp -o /tmp/a.out")

    # スコア計算のスクリプトを取得
    bucket.download_file(f"{contest_name}/vis", "/tmp/vis") # 要変更。テスター。{contest_name}/visは、S3で自分で設置した場所を指定。visは"cargo run --release --bin vis"でRustコンパイルしておく。
    os.system("chmod 777 /tmp/vis")

同時実行数が最大で10になっていた。

TooManyRequestsExceptionというエラーがよくかえってきたのですが、50個のテストケースを回していたのに最大10だったからでした。デフォルトで1000らしいですがなぜか10になっていました。

最後にChatGPTによるブログ

タイトル： AWS LambdaとAmazon S3を使用した高負荷タスクの並列化

AWS LambdaとAmazon S3を組み合わせることで、高負荷タスクを並列化し、処理効率を向上させることができます。今回は、プログラミングコンテストのジャッジシステムを構築する例として、AWS CDKとAWS Step Functionsを使って、この組み合わせを実装する方法を解説します。

1. AWS CDKとLambda関数の作成

まず、AWS CDKを使用して、タスクの各ステージを処理するLambda関数を作成します。今回は、各問題を別々に評価するためのLambda関数（evaluation-lambda）、評価結果をまとめるためのLambda関数（summary-lambda）、それらを制御するエントリポイントとなるLambda関数（entry-lambda）の3つを作成します。Lambda関数は、AWS CDKのlambda.DockerImageFunctionを使用してDockerイメージから作成します。

各Lambda関数はS3バケットに対する読み書き権限を持ち、バケット名は環境変数から取得します。

2. Step Functionsの構築

次に、AWS Step Functionsを使用してこれらのLambda関数を連携させます。Step Functionsのステートマシンは、エントリポイントのLambda関数を最初に実行し、次にマップステートを使用して評価Lambda関数を並列実行し、最後に結果をまとめるLambda関数を実行します。

3. ログの確認

Lambda関数がエラーを返す場合や、デバッグが必要な場合は、AWS CloudWatch Logsを使用してログを確認できます。CDKで作成したLambda関数は、関数名が自動生成されるため、AWS Management ConsoleのLambdaのダッシュボードから関数を見つけることができます。

4. バケットとファイルパスの確認

Lambda関数がS3からファイルをダウンロードできない場合、バケット名やファイルパスが正しいか確認が必要です。S3バケットの名称はCDKスタック名とリソース名から自動生成されるため、AWS Management Consoleから確認することができます。

5. 同時実行数の調整

Lambda関数の同時実行数が多すぎる場合、TooManyRequestsExceptionが発生する可能性があります。これは、Lambda関数のデフォルトの同時実行数（1000）を超えた場合や、Lambda関数の設定で制限された場合に発生します。

解決方法としては、AWS Management ConsoleのLambdaの設定から特定のLambda関数の同時実行数の上限を増やす方法があります。さらに、Lambda関数の上限がアカウントレベルで設定された上限（"予約されていない同時実行数"）を超えている場合は、AWSサポートに問い合わせてアカウントレベルの同時実行数の上限を増やすことも必要です。

今回の実装を通して、AWS LambdaとAmazon S3を組み合わせて、高負荷タスクを効率的に並列化する方法を学びました。この方法は、プログラミングコンテストのジャッジシステムだけでなく、データ処理やマイクロサービスの構築など、さまざまなシナリオで応用できます。

2023-01-03

「競技プログラミングの鉄則」のレビュー

競技プログラミングマラソンマッチ AtCoder C++

米田優峻さん（E869120@ICPC2022 (@e869120) / Twitter）の著書「競技プログラミングの鉄則 ~アルゴリズム力と思考力を高める77の技術~」をご恵贈いただきました。その感想です。

競技プログラミングの鉄則 (Compass Booksシリーズ)

作者:米田優峻
マイナビ出版

Amazon

素晴らしい内容で競技プログラミング初心者への最初の１冊として最もお勧めできる本です。特に、数学も得意というわけではなくプログラミング自体も初めてという方には、ダントツで一番お勧めできる本です。

本書の良い点

１．図が分かりやすい。

最初の48ページが無料公開されているので、百聞は一見にしかずということで見ていただけると良いと思います。i
www.dropbox.com
図自体分かりやすいですし全編カラーで書かれているのも良いです。段階的に説明すべきものについて無理に１枚に納めず多くの小さい図に分けて説明しているのもとても分かりやすいです。先ほどのpdfにある図の１つです。

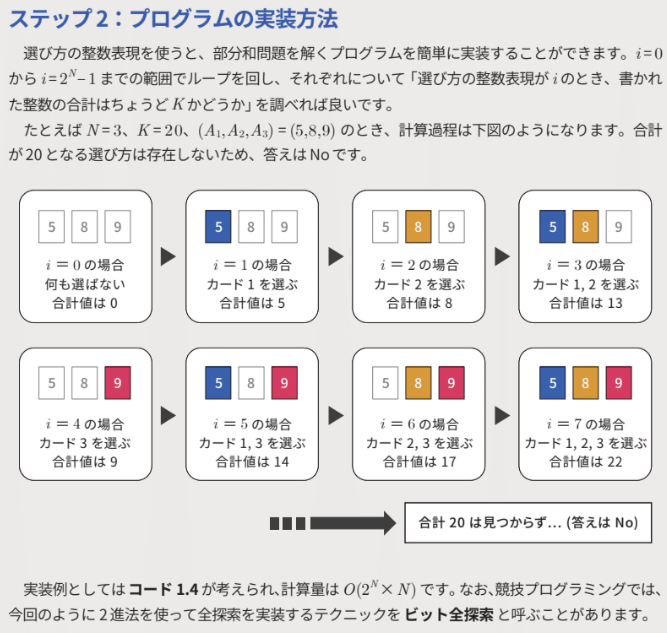
また、既に理解しているアルゴリズムでも、勘違いしたりケアレスミスしたり書くのに妙に時間かかったりすることは誰にでもあると思います。本書の分かりやすい図は、自分の中での理解をアップデートするのにとても役立ちました。簡単な問題でも「あー、たしかにこういうふうにイメージできれば、すっきり理解できるなぁ」と感じることが多かったです。

２．つまづきにくい。

頭が良いが説明が苦手な人が記事を書くと、説明の段差が大きくなりがち（例：「自明である」、「定義そのもの」、式の省略等）ですが、この本についてはそういうことはありません。特に、各節最初の例題は「無駄な部分を省き、学んでほしい部分に絞った問題」となっており、その例題まですら図で多く説明しているので、とにかく最初の１歩では絶対につまづかせないという意図を感じます。続く応用問題もほとんどの場合は例題に沿っています（でもコピペではうまくいかないちょうど良い問題）。必要に応じてヒントも書かれています。つまづきにくいです。

３．ヒューリスティックスについて取り上げてある。

できるだけ良い答えを出す系のコンテストAHC（AtCoder Heuristics Contest）についてはネットの記事はあるのですがまとまっているわけではないので、体系的に学びたい初めての人にこの本はとても良いと思います。貪欲法→局所探索法（単純山登り）→焼きなまし法のように、実際のコンテストで徐々にコードを改善していく過程に沿って書かれているので、コード量が増えがちでも分かりやすいと思います。

４．考察テクニックの章

問題のパターンは無数にあり全解法覚えるわけにもいかず自力で考察するほうが本質だと思うのですが、その考察について１章分設ける（６章）*1はとても良いと思いました。考察テクニックはもっとあると思うので、もしこの本の続編がでる場合は、さらにこの部分の分量をふやしてもらえると嬉しいです。

５．コンテンツが充実

まず問題集151問がすべてAtCoder上で利用できます。
atcoder.jp

本に載っていない分についてはgithubが用意されており、C++, Java, Pythonの3言語での解答コードも読むことができます。親切です。
github.com

解説pdfについても、本書程ではないにせよ図を駆使して分かりやすく書かれており、全216ページ（！）もあります。付録コンテンツは誰でも無料で利用できるのですが、正直ここだけでも商品になる気がします…。

本書の賛否両論ありそうな点

コードの書き方

分かりやすさのために一般プログラミングの作法については目をつむる、他の本で勉強してね、という方針は構わないと思いますが、以下の２つは気になりました。

変数の定義がmainの関数内で行われている場合と関数外で行われている場合があり、その理由が特に書かれていない。
- スタックオーバーフローを避けるために全部外に書きグローバル変数とするというのであればある意味分かりますが、そうでない例もあります。
STLに関して、説明無しで登場しているところがある（3.5章 vector）
- ここまで引っ張るより早めにどこかでSTLについて説明したほうが、生配列よりもvectorのほうが良い部分で素直にvectorを使えたので良かったかもしれません。

親切すぎる

裏を返すと、この本に慣れると

コンテストにでる、あまり素直でない問題
一足飛びの解説

などの耐性があまり付かず今後つまづくかもしれません。ただ、終章で次の教材として勧めている「競プロ典型90問」については「解説は原則１ページで簡潔にまとめられているため、分かりづらい部分もあるかもしれません。しかし、解説の行間を読むのも練習です。」と述べられており、この鉄則本については割り切って超親切にしているのかなと思いました。

同じジャンルでまとまっていて、必ずしも難度順にはなっていない。

同じジャンルのものをまとめる方式になっており、他の本では最初の方に来る「深さ優先探索」「幅優先探索」はグラフなので本書では最後のほうの9.2章・9.3章に主に取り上げています。ただ、この本は十分にわかりやすく、勉強の際には飛ばして必要な章から読むことも可能なので、必要なら飛ばし読みして良いと思います。

難度と勉強時間の目安

YouTubeで生放送しながら、本書を全部読み演習問題集の全151問を解いたのですが、33時間46分43秒かかりました。そのときの生放送は全てYouTubeのプレイリストにまとめてあります。
www.youtube.com
喋りながら問題を解くとだいぶ遅くなるのも踏まえると、おそらくAtCoder水色レベルの人なら20～25時間で全部読んで全問解けるのではないでしょうか？勉強する際の時間の目安として参考にしていただければと思います。

また著書の最終章にも書かれているのですが、米田優峻さんが本書の次にお勧めしている「競プロ典型90問」について現在解いていっています。こちらも良問が多くこれらも全て解説スライドがあり、とても親切です。
atcoder.jp

おわりに

そういうわけで自信を持ってお勧めできる本なので、みなさん購入しましょう！また、個人的な話ですが、この本がきっかけで毎朝7:00からの競プロ学習習慣がついた気がするので、このまま続けていきたいと思っています。

*1:10章の最初にも考察テクニックが書かれてあります

2022-03-28

Visual Studio 2022でC++範囲外アクセスに気づきやすくする方法

C++

配列外アクセスをしたときの比較表
Visual Studio 2022で範囲外アクセスを気づきやすくする方法５つ

はじめに
先日、Visual Studio 2022で、配列の範囲外アクセスのデバッグでハマってしまった。

constexpr int S = 20;
struct Maze
{
	Maze()
	{
		for (int y = 0; y < S; ++y)
		{
			h[y][0] = true;
			h[y][S] = true;
		}

		for (int x = 0; x < S; ++x)
		{
			v[0][x] = true;
			v[0][S] = true;	// 配列外アクセス。 v[S][x] = true が正しかった
		}
	}

	bool h[S][S+1];	// 横移動を阻む縦の壁
	bool v[S+1][S]; // 縦移動を阻む横の壁
};

定数で範囲外アクセスしているとても単純なケースなのに、なぜ警告も気づかなかったんだろう？となったので、いろいろ調べた。

配列外アクセスをしたときの比較表

コンパイルエラー・コンパイル時警告・エディタで警告
- 最高。実行前に気づける。
実行時エラー・例外中断
- まぁまぁ。実行時に気づける。実行時のabort、グローバルバッファーオーバーフロー、ヒープオーバーフロー等でとまる。
なし（オプションで実行時エラーに）
- 設定によっては、実行時に気づける。
なし
- 最悪で、範囲外のメモリを壊し動作が不定になる。未処理例外で止まる可能性もあるし、誤動作する場合もあるし、正常に動くこともある。

	Visual Studio				gcc	clang
変数の種類	Intellisense	Debug	Release	Sanitizer オプション	デバッグ寄り*1	デバッグ寄り*2
ローカル生配列	エディタで警告	1次元配列→コンパイルエラー 2次元配列→なし	なし	なし（終了時に不明の例外）	コンパイル時警告（部分的）	コンパイル時警告
グローバル生配列	エディタで警告	なし	なし	例外中断	コンパイル時警告（部分的）	コンパイル時警告
ローカル std::array	エディタで警告	実行時エラー	なし（オプションで実行時エラーに）	なし（終了時に不明の例外）	実行時エラー	実行時エラー
グローバル std::array	エディタで警告	実行時エラー	なし（オプションで実行時エラーに）	例外中断	実行時エラー	実行時エラー
ヒープ std::vector	なし	実行時エラー	なし（オプションで実行時エラーに）	例外中断	実行時エラー	実行時エラー

範囲外アクセスの参考コードはこちら

#include <iostream>
#include <array>
#include <vector>
#include <cassert>

static int sr[8] = {};
static std::array <int, 8> sa{};
static int sr2[5][8] = {};
static std::array < std::array <int, 8>, 5> sa2{};

int main() {
	int r[8] = {};
	std::array <int, 8> a{};
	std::vector < int > v(8);

	int r2[5][8] = {};
	std::array < std::array <int, 8>, 5> a2{};
	std::vector < std::vector < int > > v2(5, std::vector <int>(8));

	// 全て範囲外アクセス
	r[8] = 1;
	a[8] = 1;
	v[8] = 1;
	sr[8] = 1;
	sa[8] = 1;
	
	r2[0][8] = 1;
	r2[4][8] = 1;
	a2[0][8] = 1;
	a2[4][8] = 1;

	v2[0][8] = 1;
	v2[4][8] = 1;

	sr2[0][8] = 1;
	sr2[4][8] = 1;
	sa2[0][8] = 1;
	sa2[4][8] = 1;

	std::cerr << r[8] << '\n';
	std::cerr << a[8] << '\n';
	std::cerr << v[8] << '\n';
	std::cerr << sr[8] << '\n';
	std::cerr << sa[8] << '\n';

	std::cerr << r2[0][8] << '\n';
	std::cerr << r2[4][8] << '\n';
	std::cerr << a2[0][8] << '\n';
	std::cerr << a2[4][8] << '\n';

	std::cerr << v2[0][8] << '\n';
	std::cerr << v2[4][8] << '\n';

	std::cerr << sr2[0][8] << '\n';
	std::cerr << sr2[4][8] << '\n';
	std::cerr << sa2[0][8] << '\n';
	std::cerr << sa2[4][8] << '\n';

	return 0;
}

Visual Studio 2022で範囲外アクセスを気づきやすくする方法５つ

エラー一覧を「ビルド＋Intellisense」にする

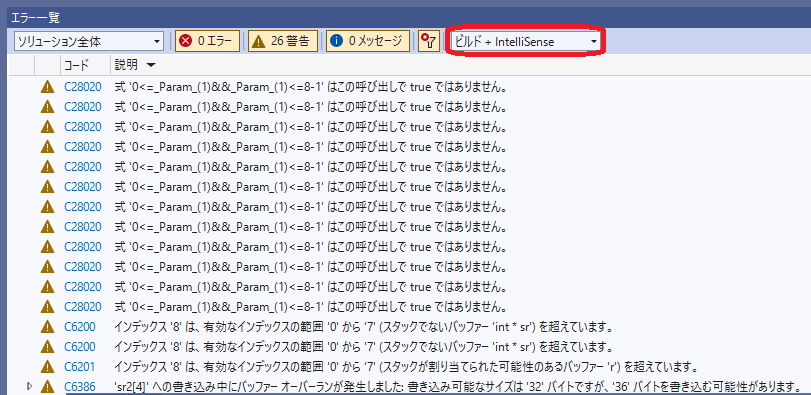
f:id:shindannin:20220328054022p:plain
f:id:shindannin:20220328054310p:plain

インテリセンスで範囲外アクセスの警告が表示されて、基本的には強力である。
- 逆にビルドの出力ログには警告すら表示されないので、それしか見ていないと気づかずに大失敗するので、要注意。今回気づかなった一番の原因はこれ。
- インテリセンスなので、すぐに表示されなかったり、なにかのきっかけでリフレッシュされず古い情報が残ったりする（おそらくMicrosoftのバグ）。ターゲットの切り替えや、コード編集後にリビルドをすると直ったりするが不確定で緩慢なこともある。

sanitizerを積極的に使う

f:id:shindannin:20220328054555p:plain
（訂正）さらに調べてみたところ、ローカル変数を使用していないコードでも終了時に常に例外（0xE0736171）が出ることが分かりました。おそらくVisual Studioの問題？
~~- ローカル変数の例外（0xE0736171）は例外設定に入っておらず、ログには情報が流れるもの中断はしないので気づきにくい。~~

- ~~中断するなら、以下のように例外設定ウィンドウで追加すればよい。ただしデバッグ情報は他のオーバーフローのように表示されない。~~

今回のような配列範囲外のミスだけではなく、ダングリングポインタ・メモリリークなども見つけることができる。

生配列よりstd::arrayがよい

ローカル1次元配列だけなぜか親切にコンパイルエラーを出してくれるが、それ以外はチェック目的ならstd::arrayが常に良い。
特にstd::arrayの2次元以上の書き方が順番が逆で、慣れないと間違えやすいが、テンプレートを使うことで緩和できる。以下のページがおすすめ。

koturn.hatenablog.com

Release版でSTLの範囲チェックしたいときは、 _CONTAINER_DEBUG_LEVEL=1 にする

f:id:shindannin:20220328055135p:plain

実行時に、Debug版だと遅すぎて問題箇所までたどり着かないとき、Release版でSTLの範囲チェックしたいときに使える。
Debug, Releaseターゲット以外に、最適化するけど範囲外チェックするデバッグ用のターゲットを用意してもよい。

devblogs.microsoft.com

インテリセンスが安定せず嫌な場合、clangを代わりに使うのがよい

clangでもgccでも、警告の種類は"-Warray-bounds"だが、結果は微妙に違う。
- Clangは、ほぼコンパイルオプションなし"clang++ -std=gnu++17"でも、コンパイル時に生配列への不正アクセスの警告をしてくれる。
- gccは、 "g++ -O2 -std=gnu++17 -Wall -g -fsanitize=undefined,address -D_GLIBCXX_DEBUG" の設定をすればコンパイル時に生配列への不正アクセスを警告してくれるが、最初の１箇所だけの警告のみで、全ての箇所の警告してくれない。

おわりに
ちなみに、今回はコンパイラオプションでの対応を取り上げたが、より複雑な問題に対応するために以下のようなツールもあります。

静的解析ツールを使う
メモリリークの検証ツールを使う（Valgrind、WindowsならAppVerifier

*1:オプション g++ -O2 -std=gnu++17 -Wall -g -fsanitize=undefined,address -D_GLIBCXX_DEBUG
バージョン g++ (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0

*2:オプション clang++ -O2 -std=gnu++17 -Wall -g -fsanitize=undefined,address -D_GLIBCXX_DEBUG
バージョン clang version 10.0.0-4ubuntu1

2022-01-10

本帰国後に、海外に置きっぱなしのお金のせいで面倒になることリスト

海外よもやま

はじめに

自分は、投資等には興味なくお金に関する面倒なことはしたくない考えなので、最低限のこと（年金・非課税投資等）しかしてなかったのですが、意図に反して5か国（米国・カナダ・フランス・香港・シンガポール）8箇所に口座や金融商品が散らばってしまいました。散らばっていることは、ある意味リスク管理には有利とも言えるのですが、以前と比べて、

節税効果はない（後述）
日本の口座に外貨のまま持つことも可能
香港にお金を置いておくのは…（実際、香港の人が口座凍結されたケースもあったし、世界情勢的には…）
もし自分に何かあったとき、全部連絡が英語だし、家族が何もできなさそう。

ということで、日本に帰国した区切りで口座等の整理を試みたのですが、いろいろと面倒があることが分かりました…。

この記事は、ほぼ自分の愚痴で人生で１回しか使わないことばかりですが、将来日本に帰国する予定がある人のチェック用にも役立つかもしれません。

お金に関することについて

クレジットカード

自動更新できない
- 居住してないとクレジットカードの更新ができない場合があります。
自動更新されてしまって損する
- 海外のクレジットカードは、日本では使えない場合が多々あります。
- 海外のクレジットカードを使うことで不正な取引との疑いで、一時停止になることは普通にあります。
- 最低使用額が指定されているケースもあります。使用額は月7000円以下のときでも7000円取られるといった状況です。クレジットカードが使用できなくなったからと言ってそのままにしておいて、思わぬ高額の使用料を毎月とられるのには注意しましょう。

Wise（旧 TransferWise）

送金手数料が安い*1ということで有名な送金サービスWiseがあります。以下の点には注意してください。

初期画面に表示されないその他の手数料もいろいろある。

以下はWiseのメッセージより

100万円を超える日本円への送金は、SWIFTにて送金されます。SWIFT送金では、TransferWiseで発生する手数料以外に受取銀行や中継銀行から課金される手数料が発生する場合がございます。この手数料はTransferWiseが課金しているものではないため、最終的な受取額を当社でも把握することができかねます。恐れ入りますが、ご理解いただければ幸いでございます

この辺は普通の銀行間の送金と一緒です。　

同一通貨の海外送金はできない。
- 違う通貨に換えることの為替手数料は大きいので、国外の銀行から日本の銀行へ同一通貨のまま送りたいことがありますがそれはできません。
- Wiseではなく普通の送金なら送れることもありますが、同一通貨のリフレクションフィーと言われる手数料がかかります。でも為替手数料よりは全然やすいです。
2000万円～3000万円以上の送金はできなくなった。
- 記事の通りです https://wise.com/gb/blog/lower-limits-for-large-transfers
- また多額の送金は、そもそもwiseで指定される口座にその金額をインターネットバンキングで送れず失敗するというケースもあります。これもwiseのメッセージで警告がでます。

租税条約や税務上の居住地に関する届け出

ちゃんと所得税等を納めて出国しても、出国後に収入を得るようなケースもあります。例えば出国後に、海外保険会社（年金用）から「租税条約に関する届出（https://www.nta.go.jp/taxes/shiraberu/taxanswer/gensen/2888.htm）」を求められたことがありました。これをやらないと海外と日本で二重課税されてしまう恐れがあります。こういう重要な連絡は普通Eメールではなく手紙でくるので、ちゃんとお金を置いているうちは住所の更新等を常にしておくべきです。
住所変更先を日本にする時や送金を行う際に、税務上の居住地に関する届け出、"Jurisdiction of tax residence"と"TIN(Tax Identification Number)"を問われます。前者は日本、後者は日本の場合はマイナンバーになります。2016年以前から海外在住の人は、マイナンバーが一度も付与されていない状態だと思うので、手続きは日本に住民票を移しマイナンバーを付与されてからになります。

外国払い小切手は、日本のほとんどの銀行では換金できない

欧米では小切手は安心できるお金の受け渡し方法としてまだ使われています。年金の掛け金の払い戻しに海外小切手が日本に送付されたのですが、これは問題がありました。日本の銀行は、ほぼ海外小切手の取り扱いを終了しています。こちらの記事（ https://yatsuyaku.com/clean_bill/ ）の通りです。唯一使えるSMBC信託銀行プレスティアにも直接伺ったのですが、手数料等を考えると海外小切手のためだけに口座を作るのはお勧めしないようでした。ちなみに、インターネットバンキングで小切手を換金する方法は考えたのですが、少なくともHSBC香港ではインターネットバンキングに対応した小切手でないと不可能でした。小切手は現地で換金しましょう。

マネーロンダリングに対して厳しくなっている

昔たまに見かけた「海外にお金を置いといて税金回避！」みたいなのは、ただの脱税になるだけです。以前よりもとても厳しくなっています。

海外の利息や株式の利益も、日本の税金の対象となります。
国外に5,000万円を超える財産を持つと、国外財産調書制度で把握されます。（https://www.smbcnikko.co.jp/terms/japan/ko/J0689.html ）国外財産調書制度とは、適正な課税の確保のため、国外に5,000万円を超える財産（預金、有価証券や不動産など）を持つ日本国内の居住者に、その内容を記した国外財産調書の提出を義務づける制度です。2014年度から始まり、現金預金、不動産、有価証券、骨董品や貴金属類まで、その年の年末時点で国外にあるすべての財産が対象となります。翌年3月15日までに税務署に提出しなければなりません。
相続税についても、国外資産についてもかかります。相続人も被相続人も10年以上住んでいる場合のみ（https://www.nta.go.jp/taxes/shiraberu/taxanswer/sozoku/4138.htm）

少し前までは、香港へHSBC香港の口座を作るためツアーがありわんさか日本人がきていたそうです（話を聞く限りそういうツアー自体かなり怪しかったようですが）が、今だに残る利点といえば「海外銀行にしかない魅力的な金融商品」がほしいときぐらいでしょうか。でも、それこそ素人では判断では難しいと思うので、あくまで自分の意見ですが、海外に投資する興味があっても普通に日本の口座を使えばよいのではないかなと思います。

口座閉鎖する意思があり、日本に戻ってくる前に口座が閉鎖できる状態であれば、現地にいる間に閉鎖してしまった方が良い

実際には、最終給与受け取り・税金支払い等で、その国を去ったあとでも一定期間口座を残しておく必要がある場合が多いですが、もし閉鎖できるなら現地にいる間に閉鎖したほうが良いと思います。インターネットバンキングでも口座閉鎖だけはできないケースがほとんどだと思います。
代替案として、「口座閉鎖はせずに、後で日本の口座にほぼ全額送金して、空っぽにしておく」という考えもあると思います。ただ、現地採用で海外から本帰国するというケースは、送金額も大きくなると思うので、やはり現地にいる間にやってしまったほうが楽だと思います。送金方法に寄らず税金に関する手続きは全て済ませておく必要があり、多額の送金では審査もあります（ https://moneykit.net/visitor/fx/fx07.html ）。日本のサポートのほうが親切なので、海外にいる間に海外の面倒は解決したほうが良いと思います。

連絡方法について

インターネットバンキング

ほとんどの手続きはインターネットバンキングでできるので、他の国に引っ越ししたときは頼みの綱です。絶対途切れさせてしまってはいけません！途切れた時に面倒にならないために、連絡先更新はすぐにやっておくのが大事です。

パスワードとIDさえ覚えておけば大丈夫に思えますが、出国後に思わぬところでアクセスが途絶えたケースを挙げておきます。
- 2段階認証が新たに追加されたが、2段階認証の登録が現地電話番号へのSMS経由のみ。
- ストックオプション用の口座で、会社連絡先しか登録されておらず、転職後にアクセス不可能。
- デジタルトークン（ちっちゃい計算機みたいなやつでパスワードがでる）の電池切れ。
一定期間インターネットバンキングでの操作がないと、限度額が減ったり口座が一時凍結になる銀行もあります。
- 最悪の場合、口座凍結解除するには、銀行に直接いかないといけない場合もあります。それはコロナ禍では無理なので、予めどういう条件で自動凍結になるかを確認しておいて、定期的にお金を動かしたりログインしておいた方がよいです。

そして一旦アクセスが途絶えてしまうと復帰は、予想外に面倒なことがあります。
- ヘルプや問い合わせ機能で、パスワード自体はリセットできても、そのあとで結局現地電話番号SMSによる認証が必要で、結局ログインできない。
- ログインの方法を問い合わせしたいのに、ログインしないと問い合わせできない。すでに仕組みとしておかしいですが、そういうのはよくあります。

出国後、連絡手段別の問題点

インターネットバンキングが途切れても、その国にいるときは簡単に復帰できますが、出国後はいろいろと難しいです。手紙・Eメール・電話・オンラインコールとなると思います。

電話（SMS）
- 現地の電話番号はすでにないので初回登録やSMSによるワンタイムパスワードを受け取れないという場合もあります。
- 現地の電話番号しかそもそも受け付けていない（ネットだと電話番号フォームに入力できない）といったこともあります。
- 問い合わせ先の電話番号が特殊な番号で、日本からは絶対かけられないケースもあります。
- 電話の問い合わせで解決できることもたまにありますが、日本のコールセンターみたいな親切はないと言ってよいですし、たらいまわしも多いです。
Eメール
- 海外-日本間のEメールはスパム扱いされて本当に届いてないこともあるので、要注意です。
- Eメール届いてない場合に、念のために確認メールだしてくるといったレベルの親切はほぼないです。せっつきましょう。
住所
- 引っ越し後に住所更新するときに、住所証明が必要な場合があります。このとき日本の住所の証明はやっかいです。
  - 住所更新時の住所の証明として、最近の公共機関の領収書等を要求されることがありますが、日本の領収書は日本語で書かれており、また「令和3年」のように西暦で書いてないこともあるので、証明にならない場合があります。説明すれば大丈夫な場合もあるので説明しましょう。
- 住所の更新をしないと最重要な連絡が届かないケースがあるので忘れずにしましょう。前述の「租税条約に関する届出」もそうですが、前に住んでた国の税金の申告書類が届くケースもあります。
手紙
- 一番遅いですが、手紙なら電話・Eメール・インターネットバンキングではできないことも、できることが多いです。
- しかし手紙の遅延もあります。届いたかどうかの確認を担当者に連絡できるようにコネクションを用意しておいたほうがいいです。
担当者（銀行の担当者・ファイナンシャルアドバイザーなど）
- 海外を去る前に担当者の連絡先を増やしておきましょう。メールもCCを複数人に増やすのが重要です。
- 海外へ送受信するメールは届いていないことが普通にあるので、1人しか担当者がいないとそれで気づかずに途切れることがあります。
- 単純に退社やご不幸等で連絡が続かなくなることもあります。
- 銀行によっては、ある程度の預金額を越えているとちゃんとした担当者がつくプレミアムサービスがあるケースもあるので、利用できるなら利用したほうがよいと思います。

日本にいる間にやっておいた方がよいこと

海外通貨が扱えてインターネットバンキングができる銀行口座
- インターネットで申し込み手続きができる銀行ありますが、結局、確認通知を日本の住所で郵便で受け取る必要があるので、日本にいる間に作っておいた方が便利でしょう。帰国の際に、海外にいる間に済ませられることが増えると思います。
- 海外通貨が扱えると、円に戻して為替手数料が取られることがないので、便利です。

おわりに

アドバイス・間違いの指摘等があったら随時更新しますのでお知らせください。

*1:以前は銀行との送金との比較表示で数%の差がでてたときもあったのですが、最近は最安の手段と比較するようになったので、送金手数料は実はあまり変わらないような気もしてきました。

2021-04-09

競技プログラミングを終わらせる人々への指摘、頑張っている人々へのアドバイス

競技プログラミング

はじめに

競技プログラミングに関連する、以下の記事が話題にあがりました。

nuc氏1つ目の記事
nuc.hatenadiary.org

chokudai氏の記事
chokudai.hatenablog.com

nuc氏2つ目の記事
nuc.hatenadiary.org

nuc氏は、元Googleのエンジニアで面接も担当されていました。現在は某医大の特別特命准教授の方で、2007年頃に東大で競技プログラミングをされていた方のようです（氏名も役職も上記の記事のリンク先で公表されています）。nuc氏の記事は、競技プログラミングに対して「我々の目的の一つは、我々が始めてしまった競技プログラミングを我々が終わらせることです。」といった強い主張が多く、これらの記事の反応をみたのですが、

競技プログラミングをしている方々が、nuc氏の主張で不安になり、特に若い世代で、競技プログラミングをやめようとしているケース
競技プログラミングを知らない方々で、nuc氏の主張を鵜呑みにして、競技プログラミングを誤解しているケース

等を見かけました。そういうわけで、なんらかのフォローをしたほうが良いと思い、この記事を書きました。

フォローの内容は以下のようになっています。

第１章　競技プログラミングは変質したのか？
第２章　競技プログラミングは変質して、悪影響を与えたのか？
第３章　競技プログラミングをがんばっている皆さんへのアドバイス

付録以下の内容は今回のフォローとは関係ないのですが、一連の記事の読者の中で混乱していた方も見受けられたので、その辺を整理したものです。ほとんどの方は興味ない内容だと思うので、飛ばされても結構です。

付録１章　nuc氏の議論方法の問題点
付録２章　nuc氏のグループは、競技プログラミングを生み出したのか？
付録３章　残る疑問

ちなみにnuc氏の記事の内容に全て反対しているというわけではありません。

「競技プログラミングだけやっていても、Googleの入社面接の対策は不十分」という主張。これは、chokudai氏・nuc氏、元記事のリンク先で登場したLillian氏、全員同じです。
おすすめの本

のあたりは正しいと思っております。

第１章　競技プログラミングは変質したのか？

nuc氏は記事の中でこのように述べています。

我々の目的の一つは、我々が始めてしまった競技プログラミングを我々が終わらせることです。

競技プログラミングは変質し、その悪影響は看過できない所まで来てしまったと思います。競技プログラミングを始めた人たちができていたことが、その少し下の世代ではみるみるできなくなっていったと思われます。少なくとも、競技プログラミングの関係者がここまで Google に通らないことはありませんでした。

そして、2007年に競技プログラミングの名前が付きます。つまり「競技プログラミング」が広まり変質したというのは AtCoder ができる2012年より前の話をしています。

「悪影響は看過できない」は断定まではしていませんが結構強めの主張だと思います。でも、そもそも悪影響を与えるような変質があったのでしょうか。これを見ていきたいと思います。

短期コンテスト

まず、昔の競技プログラミングのほうが必要な能力が鍛えられていた例がいろいろあげられていましたが、トピックごとに検討してみました。

1・打ち込むのが大変なアルゴリズムも出題されていてた。（減った）

実装量が多いがアルゴリズムがほぼ不要な問題、通称「実装やるだけ問題」については、これは確かに現代のほうが減ったと思います。

2・バックスラッシュ（変化なし）

これは昔も今も短期コンテストでほぼ出題されていないと思います。例外的に、TopCoder・Codeforces等で、2次元のフィールドの左斜め方向を表すために使わていることありました。念のため2000年以降のICPC World Finalの問題をチェックしましたがバックスラッシュを入出力に使うケースはありませんでした。

3・言語の選択（重要になった）

昔は短期コンテストで使用できる言語は数個でしたが、現在では使用できる言語が圧倒的に増えていますし、むしろ現在の競技プログラミングのほうで重要です。文字列処理が簡単にできる言語、多倍長処理が簡単にできる言語などを適切に選べば有利になります。

4・定数倍高速化（とんとん）

昔のほうがオーダーがきっちりしておらず定数倍高速化が有効だったケースが多かったというのは同意です。しかし、逆に現在は言語が増えたことで、スクリプト言語のように実行時間が遅い言語で定数倍高速化が有効なケースもでてきたので、一長一短です。また、言語が増えたことで、すべての言語でオーダーがきっちりした問題が作るのは不可能なゆえに速い言語での定数倍高速化が有効なケースもあります。ちなみに、nuc氏は「プログラミング言語の選択は影響がないように作られています。このために、1000倍くらいの定数倍は無視します」と述べていますが、そのような問題はほとんどありません。

5・クイックソートのようなライブラリーが提供するアルゴリズムについての詳細（変化なし）

ライブラリの内容が分かっていることを要求されるアルゴリズム問題はでたまに問われますが今も昔も多くはありません。例えば、クイックソートでいえば、アンチクイックソート（クイックソートキラー）の問題については、今も特にCodeforcesで含まれています。

6・出題者の気持ちを読む能力（変化なし）

必要でしょうか？これが「制約などから逆算して、適応可能なアルゴリズムを考える」という意味なのであれば、むしろ実用的な能力です。私はこちらとこちらに同意見です。出題量の意味でも変化はありません。

nuc氏は述べていないのですが、変化があるとすれば枝刈りです。

7. 枝刈り（減った）

計算量が不定な場合が多く、ICPC以外ではほとんど出題されなくなったかもしれません。

以上は問題そのものの変化についてです。

またnuc氏は、

面白くするために作られたルールだと分かっている人たちがいなくなり、そのルールとそれによる序列が絶対的なものになってしまったということです

と述べていますが、これは違います。レーティングがつかない自由な形式の短期コンテストは、現在のほうが明らかに増えてます。代表的なものとしてyukicoderががあります。
yukicoder.me
「競技プログラミングは、出題することもとてもアルゴリズムの勉強になります。完璧に出題できなくても、気軽にお互い指摘しあって向上していこうという方針で行っております。」という思想により、出題形式がかなり自由で、また「ゆるふわポイント」のように競技力以外の貢献度の指標もあります。これは明らかに「ルールとそれによる序列が絶対的なもの」と真逆です。参加者数も7000人以上います。

また、出題形式がとても自由な各種有志コンテスト（Xmas Contest 2020 - AtCoder 、お誕生日コンテスト - AtCoder）も増えました。これらは、競争用としては微妙ですが、プログラミングとしてはいろいろと勉強になります。例えば、入力が「１＋２＝？」となぜか画像で渡される問題がありましたが、短時間で画像解析をどうやるかを考えることができ、明らかにプログラミングの勉強にはなります。

ちなみに、短期コンテストそのもので良くなった点については元記事で触れられてはいないわけですが、AtCoderを初めてとした参加しやすいコンテストが増え参加への敷居が下がったため全体のレベルは上がり、さらにいろいろなアルゴリズムについて問われるようになりました。深みは増しています。

長期コンテスト・最適化コンテスト

長期コンテストや最適化のコンテストは、短期コンテストの例で述べた1～7の全てのスキルはもちろん、使用言語や計算資源も自由なことが多く、プログラミングのより幅広い知識スキルが必要になっています。そもそも実務の問題をアウトソーシングしている形のものすらあります。

各競技プログラミングサイトによって何を重視するかは違いますが、そういうコンテストは増え続けています。

SuperComputing Contest	1995～	スーパーコンピューターを使った高校生向けコンテスト
ICFPC	1998～	自由な形式の3日間チーム戦コンテスト
TopCoder Marathon Match	2006～	最適化・高速化・1人ゲームAI・機械学習など。NASA主催など、実務と直結するものも多い
CodinGame	2012～	ゲームっぽさ抜群の対戦型ゲームAIコンテスト
Google Hash Code	2014～	データが非常に大きい最適化コンテスト
Halite AI Programming Challenge	2017～	15000人以上が参加したこともある対戦型ゲームAIコンテスト
AtCoder	2017～	最適化・1人ゲームAI・ウェザーニュース社のデータ圧縮、日立・北大と量子コンピューター設計

nuc氏が記事内で、昔は良かった例として、問題が途中で変わった最適化コンテストの話を上げていますが

昔は、面白くないコンテストというのがたくさんあったのです。たとえば、線形時間アルゴリズムの最適化のコンテストで、締め切り後にフロッピーディスク内のファイルで計算が行われることが発表され、フロッピーディスクから大きなファイルを読み込むため、非同期処理をして読込み中に計算をした人が2位にダブルスコアで勝つというコンテストがありました。騙された感じはあります。ただ、本当に勉強になりました。

これについてはICFPCが代表格で、良くも悪くも現在までこういった出題傾向は続いています。

また、似たようなタイプの（面白くないコンテストかどうかは人によりますが）よりさまざまなスキルが要求されるコンテストは増え続けいています。

Google Hash Codeに至っては、30000人以上の参加者がおり、世界最大級の競技プログラミングコンテストとなっています。また、いまだに、大学や学会が独自主催の小さめのコンペティションというのも結構あります（例：http://www.jpnsec.org/files/competition2019/EC-Symposium-2019-Competition-English.html ）

まとめると、競技プログラミングは短期コンテストで傾向が少し変わったものの、全体としては大きく幅が広がったいえます。

第２章　競技プログラミングは変質して、悪影響を与えたのか？

最初に、「競技プログラミングは、面接のために作られたわけではないので、どう変質しようが競技プログラミング側には一切責任はない。」という部分は最初にはっきりさせておきます。

同じような仮説は各所で述べられていますが紹介します。（念のため、悪影響を与えたかどうかの立証責任は私にないです。）
f:id:shindannin:20210408125022p:plain

昔は競技プログラミングは、情報系の強い人や極めて頭の良い層しか知らなかった、そういう人達しか競技プログラミングをやれないほど敷居が高かった。アルゴリズムの勉強をちょっとすれば面接合格レベルに到達できた。
（以下の例だと、競プロをしていてアルゴリズムの能力だけであればGoogle面接合格レベルの人で、最終的に面接合格したのは、4人中3人で75%です）
f:id:shindannin:20210408125254p:plain

今は競技プログラミングが幅広い層に普及した。アルゴリズムの能力だけであればGoogle面接に通るレベルに到達できる人も増えたが、全体として面接合格レベルに到達できる割合が少なくなった。
（以下の例だと、競プロをしていてアルゴリズムの能力だけであればGoogle面接合格レベルの人で、最終的に面接合格したのは、9人中4人で44%です。割合は減っています。）
f:id:shindannin:20210408125309p:plain

といった現象が起きているだけだと予想します。アルゴリズム能力が上がること自体に悪影響はないでしょう。

第３章　競技プログラミングをがんばっている皆さんへのアドバイス

自分にとって、競技プログラミングは人生に欠かせぬものです。

本職はゲームプログラマーなのですが、競技プログラミングで得た能力は仕事に大きく役立っています。むしろ、仕事で役立たない分野が見当たらないくらいです。
競技プログラミングそのものが楽しいので、人生の豊かさアップにもなっています。
競技プログラミングを通じて、世代や業界を越えて、いろんな人と知り合うことができました。これも素晴らしいことです。

ただ、自分の例を挙げても、世代も環境も違いますしピンとこないと思うので、いろいろなテーマについて考えてみました。ここで書いていることの多くは、競技プログラミングに限らず成り立つことだと思っています。

なにかに熱中しているってこと自体が、素晴らしい。

何かが好きで熱中してがんばっているってことは、ベストな行動だと思います。一般的には高校生以下なら制約も少ないと思うので、迷わず熱中しましょう。
仮に、他の方に「あまり好きでない他の事のほうが役に立つよ！」と言われたとしてそれをやるとして、同じように頑張れるでしょうか？結局ダラダラやってしまうことになると思うので、好きなことに熱中したほうがいいです。
将来、自分の好きな事が他の事に変わったとしても、１つのことに熱中でき頑張れることが素晴らしいスキルなので、その経験自体が応用できます。
ちなみに、競技プログラミングの強さは全く関係ないです。自己ベストを出すために、ベストな行動をすること自体が大事です

競技プログラミングは役に立つ論

こういうのは価値判断の論題と言われていて、それぞれの人がどの価値に重きを置くかによって違ってくるので、決着がつかない論題と言われています（他の例：「男と女ではどちらが幸せか？」だったら、何をもって幸せとするかはなんとでも定義できるので議論に決着がつかない）
「競技プログラミングは役に立つ」をシェアするのは、他の方の参考になるので良いことですが、他の方に押し付ける必要はないと思います。
もし、わざわざ山を越えて、他の方が「競技プログラミングなんて役に立たないよ。むしろ悪影響だよ。」と言って来たら、それは「お前の中ではな…」と思って相手にしないほうがいいと思います。

競技プログラミングを仕事に役立たせたい人が仕事に役立たせるためのコツ

応用できないかを日ごろから考えようとすることは大事だと思います。普段の問題を解いているときでも、仕事をしているときでもいいので、応用できないか考えてみましょう。
競技プログラミングで学べるスキル「最適化（＝最小値を求める・最大値を求める）」は、平たくいうと、短期コンテストなら「一番良いのを探す」、長期コンテストなら「できるだけ良くする」という意味で、とても応用がききます。
長期コンテストであれば、仕事を外注しただけの問題がたくさんあります。どういう風に世の中で使われているのかはヒントになると思います。

競技プログラミングがおもしろすぎて、仕事を含む他の事に興味が持てない。

気持ちはとても分かりますが、上と下が参考になれば。

人生の目標が決まっていると、競技プログラミングをやる上でも迷わない。

人生の目標が決まってると優先度も決めやすいので、例えば社会人になっても優先度から時間を割り当てて競プロをするといったことができます。他の人の価値観押しつけにも惑わずに済みます。ただ人生の目標を立てるのは簡単ではありません。人によっては小中学生のころから崇高な目標を持ってる人もいるので焦りますが、ヒントを書いてみたいと思います。

崇高な目標を立てる必要はありません。まずは初期解をつくりましょう「毎日5時間競プロして、5時間ゲームして、お風呂とご飯が2時間ぐらいで、12時間ぐらい寝たい。あとはモテモテの生活で一生を終える。」ぐらいの目標でいいと思います。欲望のままに立てるのがいいと思います。
現実には、お金の制約・能力の制約・時間の制約・家族の制約・身体的制約などで、現状から目標達成までに大きなギャップができると思います。この例だとお金が1億円ぐらい必要な気がします。
そのギャップを埋めるに当たって妥協するのも途中の目標としては悪くないと思いますが、組み合わせを考えてみると妥協量を減らせるケースがあります。例えば、「5時間競プロして、5時間ゲーム」を組みあわせて、「ゲームAIを作る仕事を8時間する。残り2時間を競プロとゲーム」という風にすると、競プロ欲とゲーム欲もある程度も満たせる上にお金も入ってくるので、より現実的になり、最終目標にも近づけます。
また、目標を改善したい場合は、「仮に目標が全部達成できたとして、それで人生本当に満足か？」を考えると良いと思います。「毎日5時間ゲームするのも楽しいけど、せっかくならもっと時間を増やしてプロゲーマー目指すか！」みたいに考えられるといいです。
子供の頃に好きだったは、その人の本能的な欲求だと思うので、人生の目標ヒントはあるかもしれません。

Googleに入社したい方へ

なんでも１次情報が大事です。競技プログラミング勢で現役でGoogleで働いている方はかなりいるので、相談するのであればそういう方々に相談する方が良いと思います。また、YouTube上にGoogle自身が就職のためのいろいろな情報を載せています。
www.youtube.com
www.youtube.com

nuc氏の記事によると性格はあまり関係ないとのことでしたが、現役Googleのエンジニアの方の情報によると、最近は技術以外なものも求められるとのことでした。
careersonair.withgoogle.com （要登録）Googleyness & Leadership で検索してもいろいろと出てきます。謙虚さやリスペクトも大事みたいです。

以上、ここまでが競プロに関していいたいことでした。ここから先は読み飛ばしても構いません。

付録１章　nuc氏の議論方法の問題点

[1] 自分の主張を読み取れないのは相手の責任にする。

nuc氏の1つ目の記事での主張です。

[A] 競技プログラミングは、東京大学競技プログラミング同好会2007年春台湾合宿から始まります。それまで、プログラミングコンテストは開催されてきましたが、競技プログラミングの名前が使われたのはこの合宿がはじめてで、このとき一つのジャンルが生み出されたのです。

[B] 我々の目的の一つは、我々が始めてしまった競技プログラミングを我々が終わらせることです。

どちらも断定しています。[A][B]を信用して正しいものとし解釈すると、nuc氏の主張は

「競技プログラミングという一つのジャンルを生み出したのは我々（＝nuc氏を含めた合宿参加者）であり、我々の目的の一つは、競技プログラミングを終わらせること。」

となります。ジャンルを生み出した人がそれを終わらせると言ったら、ジャンルを丸ごと終わらせるという風に解釈するのが自然です。しかし、nuc氏の2つ目の記事によると、実際の意味は、

で、この「競技プログラミングを終わらせなければ」における「競技プログラミング」というのは、もともとは、今回の模擬面接をした3人の周りの人たちの間では、競技プログラミング同好会・クラブやその周辺の活動を指すわけです。そりゃそうじゃないですか、「競技プログラミングをする」という表現は当時はなくて、「プログラミングコンテストに出る」と言っていたわけです。だから、競技プログラミングといえば、自分たちが大学生の頃の集まりを指すわけです。「学生時代のバンドを終わらせなければ」と置き換えたら意味が通じるでしょうか。つまり、自分たちの大学生・大学院生の頃を反省して、とても大事なことをやり忘れてきたのでやり終わらなければいけない、ということです。

「そりゃそうじゃないですか」と理解できるのが当然のごとく言っていますが、2012年以前に活動は終わっているわけですし、終わらせる対象が「当時の競技プログラミング同好会・クラブやその周辺の活動」と限定的だというのは、思いこみをなしにそう確定することはできません。

[2] 相手の主張は自分の思いこみでより悪く解釈する。

chokudai氏は記事で、[C]と[D]を主張しています。

[C] 「競技プログラミングをしている」と言ったら、非常にありがたいことに、殆どの人がAtCoderに取り組んでいると思います。日本における「競技プログラミング」は、「AtCoder」と言い換えても、さほど問題がないかと思います。

[D] 昔の競技プログラミングがどんなものだったか知りませんが（とはいえ、記事で書かれていた2007年に僕は競技プログラミングにすでに行っていましたが）、今の日本の競技プログラミングの主流であるAtCoderは、このようなものになっています。

[C]についても断定まではしてません。[D]では今の日本の競技プログラミングということで、昔の競技プログラミングと明確に区別しています。

AtCoderは競技プログラミングに含まれる（競技プログラミングの一部である）ことは明らかで、[C]で言い換えても問題ないというのは
「競技プログラミングが終わる」ならば「AtCoderが終わる」
のようなケースのことを指しているのかなと解釈しました。これは真です。

これに対してnuc氏は2つ目の記事で以下のように解釈しました。

別に「競技プログラミング」という単語を商標登録していたわけでもないですから、その後、誰が使うのも自由です。ただ、さすがに、個人の代名詞や会社の代名詞のようになっていると思っている人がいることには私は気が付かなかったわけです。

「ちょくだい」は、東京大学「ちょくだい」同好会2007年春台湾合宿から始まります。
「ちょくだい」は変質し、その悪影響は看過できない所まで来てしまったと思います。
我々の目的の一つは、我々が始めてしまった「ちょくだい」を我々が終わらせることです。
「AtCoder」は、東京大学「AtCoder」同好会2007年春台湾合宿から始まります。
「AtCoder」は変質し、その悪影響は看過できない所まで来てしまったと思います。
我々の目的の一つは、我々が始めてしまった「AtCoder」を我々が終わらせることです。

これはchokudaiさんの主張に全く沿っていません。まず[D]で昔の競技プログラミングと明確に区別はしているのに、nuc氏は昔の競技プログラミングをAtCoderと置き換えてしまっています。これらの文は一目みたら意味がわからず、読者でこう解釈した人はほぼいないと思われます。特に、昔の「競技プログラミング」を「ちょくだい」と置き換えるのについては、そのような主張はなく、全く意味が分かりません。

そりゃそういう風にいわれたら怒ります。ごめんなさい。だけど、破産させる気も抹殺する気もありませんでした。というよりも、こう読まれるのにあらかじめ気がつけというのは、正直無理です。

正直無理とは言っていますが、それはnuc氏が勝手に「昔の競技プログラミング」を「ちょくだい」に置き換えたために起こった自作自演なのに、相手の責任にしています。さすがにこれはnuc氏に悪意があると思われて致し方ありません。

また[1][2]からダブルスタンダードであり、公平性がなく、説得力がないと思います。

[3] 分かりやすく書く気がない

chun さんに、このようなことをお伝えするのは本当にお耳汚しなのですが、散逸は意図的です。私の経験則で「誰にとっても新しい情報」のメッセージを広く伝えたいときには、「詳しい人は同意するが、そうでない人は違和感を感じる内容」を加えるんです。そうすると、人は、「新しい情報の真贋を、周囲の情報から判断しようとする」ので、一部の人に認知負荷がかけられます。こうすることで、根拠と結論が噛み合わない支離滅裂な発言も出てきて広まると認識しています。

バズるのには確かに成功しましたが、真摯でないと思います。自分だったら、一意に解釈できない記事を書いて誤解されたら、自分の責任だと思っていますが…。

またマウントを取るタイプの人が、このような手法をとると、書いた側が常勝してしまうので、基本相手にしないほうが良いと思います。

違和感がある主張に対して、書いていないことを読みとらないようにしてると、「普通に考えてそんなわけない」
違和感がある主張に対して、辻褄があるように書いていないこと仮定すると、「思いこみ。文章を読む訓練をしていない人にありがち」

[4] 不遜

[1][2]については、単に議論についてのスキル不足な場合でも起こりえます。人間は誰でも間違いがあると思うので、記事の主張に間違いがあったとしても、それは冷静に問題点を修正していけばよいだけだと思います。
しかしnuc氏の記事は謝っている内容にはなっていないし、相手を悪く解釈して、嫌味っぽい言い方が多くあり、この記事を読んでnuc氏が心から謝っていると解釈する人はほぼいないと思います。（chokudai氏はもう関わりたくないので大人の対応をしているだけかと思います）

ちょくだいさん、ごめんなさい。(ちょくだいさんが中高の後輩で、中学校一年生や中学校二年生の頃の印象からアップデートされていないことも行き違いの原因かと思いますので、この書き方にいたします。)

本文が謝っている態度にもみえないですし、大人に対して、中学校一年生や中学校二年生かのように話かけている時点で相手を馬鹿にしていると思いますが…。とても失礼だと私は思いました。

さらに、

ここで残念なお知らせがあります。とある医学部教授から「読んだよー。文章はいいけど、お前が卒業生をひょいひょい適当にエンジニアにすると教授会で問題になることがあるから、するんだったら出来の悪いのにしてよね。いいね。ほんと頼むよ。特にそこにいる生徒会長みたいなのはだめだから。」ということなので、今後は、あらかじめ「出来が悪いかを問い合わせる」約束をしてきました。

「出来が悪いかを問い合わせる」、自分はこういうのに同意するような人には教わりたくはないです。この医学部教授も問題だと思いますが…。

こういうのを見ると、最初の記事のタイトル「Twitter で医師を拾ってきて Google のソフトウェアエンジニアにするだけの簡単なお仕事」の「拾ってくる」という表現ネタではなく、上から目線で本当に失礼なだけな人にも見えてきます。

その他

もし、どなたかがnuc氏は議論することになった場合は、最初に議論のマナーを守っていただけるように約束してからのほうがいいと思います。特に4. 注意点の部分
http://www.ritsumei.ac.jp/ir/ir-navi/common/pdf/technic/technic_text_09_2019.pdf

付録２章 nuc氏のグループは、競技プログラミングを生み出したのか？

nuc氏は競技プログラミングに対して責任感や使命感を感じているようなので、今回のような行動を起こしたともいえます。しかし、そもそも競技プログラミングを始めたのでしょうか？始めたのでなければ終わらせる必要もないので、なにもせず平和に終わっていたと思います。

まず本題の前に、nuc氏の指す「我々」が、競技プログラミング*1というージャンルを生み出したというのは、competitive programmingはすでに存在していたので間違いです。"competitive programming"の日本語訳を考えたということであれば合っています。「ージャンルを生み出した」は間違いというのは自明ではありますが、嘘を言っていることには違いないので反省はしてください。

自分の意見ですが、「nuc氏の指す『我々』が2007年に競技プログラミングという一つのジャンルが生み出した」のが、「nuc氏の指す『我々』が2007年以降の競技プログラミングに大きく影響を与えた」という比喩であったとしても疑問が残ります。それは以下の理由からです。

最大規模の大学対抗プログラミングコンテストICPCには、日本のチームは1999年から参加しています。ACM国際大学対抗プログラミングコンテスト - Wikipedia
2004年の時点で大学の垣根を越えた交流が行われていたようです。 FrontPage - ICPC OB/OG の会　
2007年の時点でTopCoderの日本語記事があり、大学の大会ICPC経由でなく世界的なプログラミングコンテストTopCoderに参加することもできました。私はこのルートで社会人からはじめました。TopCoderで世界と渡り合う日本IBMの異才――夷藤勇人 - ITmedia エンタープライズ
2007年頃に、東大独自で影響を与えた可能性があるとすれば、東京大学プログラミングコンテスト（UTPC）は2008年から開催されています。ただし、nuc氏本人は参加していません。東京大学プログラミングコンテスト2008 東京大学プログラミングコンテスト2009 2007年頃の東大の情報については資料が少ないので、もし詳しい情報を知る方がいれば教えてください。

ただ、nuc氏の指す競技プログラミングを生み出し終わらせようとしているメンバーが曖昧なので、確定はできません。

付録３章　残る疑問

nuc氏の指す「競技プログラミングという一ジャンルを生み出した我々」「競技プログラミングを終わらせる我々」が、台湾合宿メンバー全員なのか、nuc氏＋面接の講師役2人の計3名だけなのか、今だに分かりません。もし違うのであれば、当時の状況などを知る人を教えていただけると助かります。

また、

Q1. 競技プログラミングを始めたメンバーはだれか？
Q2. 競技プログラミングを終わらせようとしているメンバーはだれか？始めたメンバーと同じか？
Q3. 競技プログラミングを終わらせる活動に、競技プログラミングを始めたメンバーはどれぐらい賛同しているのか？
Q4. 競技プログラミングを終わらせる活動は、結局何をやることなのか？（「自分たちの大学生・大学院生の頃を反省して、とても大事なことをやり忘れてきたのでやり終わらなければいけない」とありますが…）

このあたりをはっきりさせないと、これ以上議論が進まなそうです。

2007年の東大の状況は分からないのですが、2008年からはUTPCというコンテストがあり、参加者や作問者が見れます。

私自身、このメンバーの半分ぐらいは知っていると思うのですが、終わらせようとしているのに賛同している人がどれぐらいいるのか疑問が残ります。

*1:ちなみに、「競技プログラミング」という訳語自体も、実はすぐには広まりませんでした。当時、ほとんど「プログラミングコンテスト」という呼び方をしていたと思います。Googleトレンドの検索結果。プログラミングコンテストだと主語が大きく、それこそ他のプログラミングの存在を無視している感がある、そのかわりに「競技プログラミング」という呼び名が使われるケースが増えたと予想しています。→追記:情報をいただきました競技プログラミングという言葉の誕生 - MAYAH

2021-03-06

焼きなまし法のコツ Ver. 1.3

TopCoder マラソンマッチ

焼きなまし法そのものの解説は少しだけにして、焼きなまし法の使い方のコツをメインに書こうと思います。

焼きなまし法の概要

最適化（=最大値か最小値を求める）の手法の１つです。以下は擬似コードです。

あらかじめ、計算する時間を決める。
以下のスコープ内のコードを時間経過するまで繰り返す。
{
    適当に、次の状態（近傍）を選ぶ。
    (1) 次の状態のスコアが、今の状態のスコアより良くなった場合は、常に、状態を次の状態にする（遷移）。
    (2) 次の状態のスコアが、今の状態のスコアより悪くなった場合でも、ある確率で、状態を次の状態にする。
        確率は以下のように決める。
       (2.A) 序盤(経過時間が0に近いとき)ほど高確率で、終盤ほど低確率。
       (2.B) スコアが悪くなった量が大きければ大きいほど、低確率。
}
最後に、今までで一番スコアのよかった状態を選ぶ。

次の状態が悪くてもそれを選ぶ可能性がある(2)の部分が、焼きなまし法の最大の特徴です。

「状態」「スコア」というのがピンとこないかもしれませんが、

もし、巡回セールスマン問題であれば、
- 状態 →ルート
- 次の状態（近傍）→元のルートをちょっとだけかえてみたルート
- スコア →総距離
もし、y=f(x)の最大値を求める問題であれば、
- 状態 →x
- 次の状態（近傍）→ x' = x + a (aは小さめの値)
- スコア →y

といったかんじです。

サンプルソースコード

AtCoderのコンテストIntroduction to Heuristics Contest - AtCoderで、スケジューリング問題が出題されました。この問題は焼きなまし法が効果的です。C++でのサンプルを2つ用意しました。変数名は問題に合わせています。

サンプル1

単純な焼きなまし法。1165人中400位相当の解法です。焼きなまし法の本質は、// 焼きなまし法（ここから）の部分です。
AtCoderの提出コード

ソースコードを開く

#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include <cassert>
#include <climits>
#include <cmath>

using namespace std;
using namespace chrono;

// 0以上UINT_MAX(0xffffffff)以下の整数をとる乱数 xorshift https://ja.wikipedia.org/wiki/Xorshift
static uint32_t randXor()
{
    static uint32_t x = 123456789;
    static uint32_t y = 362436069;
    static uint32_t z = 521288629;
    static uint32_t w = 88675123;
    uint32_t t;

    t = x ^ (x << 11);
    x = y; y = z; z = w;
    return w = (w ^ (w >> 19)) ^ (t ^ (t >> 8));
}

// 0以上1未満の小数をとる乱数
static double rand01()
{
    return (randXor() + 0.5) * (1.0 / UINT_MAX);
}

const static int NUM_TYPES = 26; // コンテストの種類数

// 全体のスコア（今回の問題のスコア）
static int getFullScore(const int D, const vector <int>& C, const vector <int>& T, const vector<vector<int>>& S)
{
    int score = 0;

    vector <int> last(NUM_TYPES, 0);

    for (int d = 0; d < D; d++)
    {
        const int j = T[d];
        last[j] = d + 1;
        for (int t = 0; t < NUM_TYPES; t++)
        {
            score -= (d + 1 - last[t]) * C[t];
        }
        score += S[d][j];
    }

    return score;
}

int main()
{
    //  入力
    int D;
    cin >> D;
    vector<int> C(NUM_TYPES);
    for (int &c : C)
    {
        cin >> c;
    }

    vector<vector<int>> S(D, vector<int>(NUM_TYPES));
    for (auto &s : S)
        for (auto &x : s)
        {
            cin >> x;
        }

    // 初期解
    vector<int> T(D);   // T[d] d日目に開くコンテスト
    for (int d = 0; d < D; d++)
    {
        T[d] = d % NUM_TYPES;
    }

    // 焼きなまし法（ここから）
    auto startClock = system_clock::now();
    int score = getFullScore(D, C, T, S);   // 現在のスコア
    int bestScore = INT_MIN;                // 最高スコア
    vector <int> bestT;                     // 最高スコアを出したときのT

    const static double START_TEMP = 1500; // 開始時の温度
    const static double END_TEMP = 100; // 終了時の温度
    const static double END_TIME = 1.8; // 終了時間（秒）

    double time = 0.0;   // 経過時間（秒）
    do
    {
        const double progressRatio = time / END_TIME;   // 進捗。開始時が0.0、終了時が1.0
        const double temp = START_TEMP + (END_TEMP - START_TEMP) * progressRatio;

        // 近傍 : d日目のコンテストをtに変えてみる。d,tはランダムに選ぶ。
        const int d = randXor() % D;
        const int t = randXor() % NUM_TYPES;
        const int backupT = T[d];
        int deltaScore = 0; // スコアの差分 = 変更後のスコア - 変更前のスコア
        deltaScore -= getFullScore(D, C, T, S);
        T[d] = t;   // 変更
        deltaScore += getFullScore(D, C, T, S);
        const double probability = exp(deltaScore / temp); // 焼きなまし法の遷移確率

        if (probability > rand01())
        {
            // 変更を受け入れる。スコアを更新
            score += deltaScore;
            if (score > bestScore)
            {
                bestScore = score;
                bestT = T;
            }
        }
        else
        {
            // 変更を受け入れないので、元に戻す
            T[d] = backupT;
        }

        time = (duration_cast<microseconds>(system_clock::now() - startClock).count() * 1e-6);
    } while (time < END_TIME);
    // 焼きなまし法（ここまで）


    // 出力
    for (int t : bestT)
    {
        cout << t + 1 << endl;
    }
    cerr << "bestScore: " << max(0, bestScore + 1000000) << endl;

    return 0;
}

サンプル2

やや複雑ですが、かなり改善した焼きなまし法。1位相当の解法です。
AtCoderの提出コード

ソースコードを開く

#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include <cassert>
#include <climits>
#include <cmath>

using namespace std;
using namespace chrono;

// 0以上UINT_MAX(0xffffffff)以下の整数をとる乱数 xorshift https://ja.wikipedia.org/wiki/Xorshift
static uint32_t randXor()
{
    static uint32_t x = 123456789;
    static uint32_t y = 362436069;
    static uint32_t z = 521288629;
    static uint32_t w = 88675123;
    uint32_t t;

    t = x ^ (x << 11);
    x = y; y = z; z = w;
    return w = (w ^ (w >> 19)) ^ (t ^ (t >> 8));
}

// 0以上1未満の小数をとる乱数
static double rand01()
{
    return (randXor() + 0.5) * (1.0 / UINT_MAX);
}

const static int NUM_TYPES = 26; // コンテストの種類数

// 全体のスコア（今回の問題のスコア）
static int getFullScore(const int D, const vector <int>& C, const vector <int>& T, const vector<vector<int>>& S)
{
    int score = 0;

    vector <int> last(NUM_TYPES, 0);

    for (int d = 0; d < D; d++)
    {
        const int j = T[d];
        last[j] = d + 1;
        for (int t = 0; t < NUM_TYPES; t++)
        {
            score -= (d + 1 - last[t]) * C[t];
        }
        score += S[d][j];
    }

    return score;
}

// d日目のコンテストT[d]を開いたときのスコア増分
static int getContestScore(const int d, const int D, const vector <int>& C, const vector <int>& T, const vector<vector<int>>& S)
{
    const int t = T[d];
    int score = S[d][t];

    int prev = d - 1;   // d日目以前に開かれる同じコンテストの日
    while (prev >= 0 && T[prev] != t)
    {
        prev--;
    }

    int next = d + 1;   // d日目以降に開かれる同じコンテストの日
    while (next < D && T[next] != t)
    {
        next++;
    }

    // sum(x) = x*(x+1)/2 つまり1,2...,xまでの等差数列の和とすると
    //	score -= sum(next - prev -1) * (-C[t]);                       // ... (1)
    //	score += sum(day  - prev -1) + sum(next - day  -1) * (-C[t]); // ... (2)

    // p---------n コンテストをおく前
    //  123456789 // ... (1)

    // p---d-----n コンテストをおいた後
    //  123 12345 // ... (2) 

    score += (next - d) * (d - prev) * C[t];    // (1)と(2)を計算すると、簡単になる。

    return score;
}

int main()
{
    auto startClock = system_clock::now();

    //  入力
    int D;
    cin >> D;
    vector<int> C(NUM_TYPES);
    for (int &c : C)
    {
        cin >> c;
    }

    vector<vector<int>> S(D, vector<int>(NUM_TYPES));
    for (auto &s : S)
        for (auto &x : s)
        {
            cin >> x;
        }

    vector<int> T(D);   // T[d] d日目に開くコンテスト
    for (int d = 0; d < D; d++)
    {
        T[d] = d % NUM_TYPES;
    }

    int score = getFullScore(D, C, T, S);   // 現在のスコア
    int bestScore = INT_MIN;                // 最高スコア
    vector <int> bestT;                     // 最高スコアを出したときのT

    const static double START_TEMP = 1500; // 開始時の温度
    const static double END_TEMP   =  100; // 終了時の温度
    const static double END_TIME   =  1.8; // 終了時間（秒）

    double temp = START_TEMP;   // 現在の温度

    long long steps;    // 試行回数
    for (steps = 0; ; steps++)
    {
        if (steps % 10000 == 0)
        {
            const double time = duration_cast<microseconds>(system_clock::now() - startClock).count() * 1e-6;   // 経過時間（秒）
            if (time >= END_TIME)
            {
                break;
            }

            const double progressRatio = time / END_TIME;   // 進捗。開始時が0.0、終了時が1.0
            temp = START_TEMP + (END_TEMP - START_TEMP) * progressRatio;
        }

        if (rand01() > 0.5)
        {
            // 近傍1 : d日目のコンテストをtに変えてみる
            const int d = randXor() % D;
            const int t = randXor() % NUM_TYPES;
            const int backupT = T[d];
            int deltaScore = 0;

            // 変更前のd日目のコンテストのスコアを引き、変更して、変更後のコンテストのスコアtを足す。
            deltaScore -= getContestScore(d, D, C, T, S);
            T[d] = t;
            deltaScore += getContestScore(d, D, C, T, S);
            const double probability = exp(deltaScore / temp); // 焼きなまし法の遷移確率

            if (probability > rand01())
            {
                // 変更を受け入れる。スコアを更新
                score += deltaScore;
                if (score > bestScore)
                {
                    bestScore = score;
                    bestT = T;
                }
            }
            else
            {
                // 変更を受け入れないので、元に戻す
                T[d] = backupT;
            }
        }
        else
        {
            // 近傍2 : d0日目のコンテストとd1日目コンテストを交換してみる
            const int diff = randXor() % 10 + 1;    // d0とd1は10日差まで
            const int d0 = randXor() % (D - diff);
            const int d1 = d0 + diff;

            int deltaScore = 0;

            // 変更前のd0日目とd1日目のコンテストのスコアを引き、変更後のd0日目とd1日目のコンテストのスコアを足す
            deltaScore -= getContestScore(d0, D, C, T, S);
            deltaScore -= getContestScore(d1, D, C, T, S);
            swap(T[d0], T[d1]);
            deltaScore += getContestScore(d0, D, C, T, S);
            deltaScore += getContestScore(d1, D, C, T, S);

            const double probability = exp(deltaScore / temp); // 焼きなまし法の遷移確率
            if (probability > rand01())
            {
                // 変更を受け入れる。スコアを更新
                score += deltaScore;
                if (score > bestScore)
                {
                    bestScore = score;
                    bestT = T;
                }
            }
            else
            {
                // 変更を受け入れないので、元に戻す
                swap(T[d0], T[d1]);
            }
        }
    }

    // 出力
    for (int t : bestT)
    {
        cout << t + 1 << endl;
    }
    cerr << "steps: " << steps << endl;
    cerr << "bestScore: " << max(0, bestScore + 1000000) << endl;

    return 0;
}

焼きなまし法のコツ

★が多いほど、重要だと思っています。

1. 高速化

試行回数が多いほど、スコアが伸びる可能性があります。基本的にはボトルネックを調べて、そこを高速化しましょう。だいたい以下のところがボトルネックになるでしょう。

★★★★ プロファイルして、計算時間がかかっているボトルネックを探す

2021/03/06 追加しました。
焼きなまし法に限らず、マラソンマッチに限らず、プログラミング一般であらゆる高速化の前にやるべきことです。プロファイルの仕方はOSやツールにより違いますが、例えばVisual Studioなら「デバッグ」→「パフォーマンスプロファイラ」で、一発でできます。思わぬところがボトルネックになってることも多いので、絶対しましょう。
f:id:shindannin:20210306115133p:plain

★★★★ 高速化がどれだけ効果的か検討する。

重要です。ためしに10秒だけやってる計算を、あえて100秒とかに伸ばしてみて、結果がどうなるか見てみましょう。

時間をかければかけるほどスコアが伸びる
- 高速化しよう＆スコアが素早く伸びるように次の状態を決めよう。山登り法に変えるのも良い。
時間をかけてもスコアが伸びない & スコアが高い
- 最適解がでてる可能性が高い。計算を打ち切って、余った時間を他に使う
時間をかけてもスコアが伸びない & スコアが低い
- 次の状態の決め方、スコア関数の見直しを再検討する。焼きなまし法を使わない法がよいときもあるのも忘れずに。

こういった実験は自分のPCで行うわけなので、並列化などを行い計算リソースも存分に使ってよいです。

★★★★ 変更がある変数だけを保存して、戻す

先ほどのコードだと、

        const int backupT = T[d];

        // （略）    

        {
            // 変更を受け入れないので、元に戻す
            T[d] = backupT;
        }

の部分です。変更した、T[d]の部分だけをバックアップしておけば、元に戻せます。T全体を保存する必要はありません。

★★ 逆の手で、戻す

逆の手をやれば、前の状態に高速に戻せるのであれば、そうしましょう。例えば、上下左右に駒をうごかせるというパズル問題であれば、左に動かした後であれば、右に動かせば、戻せます。また、2つをswapするといった場合は、もう1回swapすれば戻せます。

★★★★ スコア関数の高速化

スコア関数の求め方は問題によって大きく異なるので、計算時間も異なってきます。ボトルネックになってたら高速化しましょう。
また、スコア関数の正確さを犠牲にしてでも、高速化したほうが良い場合もあります。１つのコツとして覚えて置きましょう。

★★★★ スコア差分計算時の打ち切り

2021/03/06 追加しました。
スコア差分計算の途中で、差分がすでに大きくマイナスになっていて、もうその後計算し続けていても絶対に遷移の受理確率がほぼ0っぽいのであれば、差分計算を打ち切って高速化することができます。焼きなまし法は遷移が成功するケースより遷移が失敗するケースが多く、失敗するケースをさっさと打ち切ることができれば高速化につながることが多いです。
また問題によっては、スコア差分の上界・下界が分かるケースもあり、これらが短時間で求められるのであれば、それもスコア差分計算の打ち切りに使用可能です。例えば、Google Hash Code 2021の練習問題では、10000ビットのORを取り、(ビットが1の数)の2乗がスコアになる問題がありました。10000ビットのORはそれなりに時間がかかりますが、

（ほんとは10000ビットある）

1110010101001   （1が7個）
0011000101000   （1が4個）  
↓ OR
1111010101001   （1が9個。つまり81点）

と実際にORをとらずとも、

1110010101001   （1が7個）
0011000101000   （1が4個）  
↓ OR
???????????????    （1が最小で7個、最大で11個、つまり49点～121点のあいだ）

というのが分かれば、打ち切り時の計算の参考になります。

★★★ 状態を変えずにスコア差分を計算する

2021/03/06 追加しました。
状態の更新をする部分がボトルネックとなっている場合は、
サンプル2の以下のような書き方よりも、

状態を変える
差分スコアを求める
遷移確率probabilityを求める
if (probability > rand01()) // 遷移条件を満たすか
{
  // 変更を受け入れる。スコアを更新
}
else
{
  // 変更を受け入れないので、状態を元に戻す
}

以下のような形のほうが良いです。なぜなら状態遷移しないときに状態更新の計算を省けるからです。また、スコア差分計算時の打ち切りを行う際も、打ち切った際に状態を戻す必要がないため、この形のほうが恩恵が大きいです。

状態を変えずに差分スコアを求める
遷移確率probabilityを求める
if (probability > rand01()) // 遷移条件を満たすか
{
  // 変更を受け入れる。スコアを更新。状態も更新
}

ただ、短時間で書けるほうは大抵サンプル2の形なので、まずはサンプル2の形で書いて、その後この形に持っていくのが良いと思います。

★★ C言語のrand()を使わない。

C言語のrand()は遅いので、高速なxor128を使いましょう。

unsigned int randxor()
{
    static unsigned int x=123456789,y=362436069,z=521288629,w=88675123;
    unsigned int t;
    t=(x^(x<<11));x=y;y=z;z=w; return( w=(w^(w>>19))^(t^(t>>8)) );
}

★ 時間計測の関数を呼びすぎない。

サンプル2のように、10000回に1回だけ時間計測をするという方法があります（時間計測の関数はsystem_clockを使えば近年は十分速いですが）。時間計測以外の値でも、毎回計算する必要がないものがあればここで計算してしまいましょう。

    long long steps;    // 試行回数
    for (steps = 0; ; steps++)
    {
        if (steps % 10000 == 0)
        {
            const double time = duration_cast<microseconds>(system_clock::now() - startClock).count() * 1e-6;   // 経過時間（秒）
            if (time >= END_TIME)
            {
                break;
            }

ただ、TopCoderだとこの回数を増やしすぎて、制限時間オーバーしてしまうという可能性もあります。そういった点も考えて、適切な回数おきに時間をはかるようにしましょう。残り時間が少なくなったら、ループ回数を減らすといった安全策をとる方法もあります。

2. 次の状態（状態近傍）をどう決めるか？

ここは鍵になる部分ですが、コツとしてまとめるのは難しいところですね…。

★★★★ スコアが改善しやすくなるように、次の状態を選ぶ。

これは、問題ごとによく考えて対処しなければいけないので、あまり「コツ」というかんじではないのですが…。

[問題]
タスク数aの仕事Aと、タスク数bの仕事Bがある。
作業員はx人いて、それぞれ、1時間あたりにこなせる仕事Aのタスク数と、仕事Bのタスク数は決まっている。
ただし、仕事Aの仕事Bのどちらかしか行うことができない。
仕事Aと仕事Bの両方が終わるのに時間が最小になるように、作業員を仕事Aか仕事Bのどちらかに割り当てよ。

焼きなまし法で解くなら、まず最初にてきとーに作業員をA,Bに割り振り、ここからスコア＝作業時間として、改善させていきます。こういった問題を解くときに、次の状態として以下の２つを考えてみましょう。

移動：ある作業員をA→B または B→A に移動させる。
交換：Aの作業員の誰かと、Bの作業員の誰かを交換する。

移動２回は交換になることもあるので、とりあえず移動をさせておけば、交換もたまにしてくれるし良さそうに見えますが、そうとは限りません。この場合は、交換を主に行い、たまに移動させるぐらいがちょうど良いと思います。移動では、人数が偏り、片方の仕事の作業時間が増えやすくなります。２回移動すれば、交換になって、作業時間が減る可能性がありますが、

移動：良スコア → 悪いスコア → とても良いスコア
交換：良スコア　　 → とても良いスコア

と考えると、移動だけだと、スコアが悪い状態を経由しないとダメなので、運がよくないと、とても良いスコアまで辿りつけません。その点、交換ならば、人員が偏った悪いスコアになりやすい状態をスキップできるので、スムーズにとても良いスコアまで改善できます。

もちろん、正しい人数割り当てもしなければいけないので、移動も少しは試したほうがいいですが、こういった点も考えて次の状態を決めると、スコアが改善しやすくなります。

★★★★ 近傍の種類を増やす

2021/03/06 追加しました。

近傍の種類は多くあればあるほど良いです。上記のサンプル2のコードには、近傍が２種類用意されています。

            // 近傍1 : d日目のコンテストをtに変えてみる
            const int d = randXor() % D;
            const int t = randXor() % NUM_TYPES;

            // 近傍2 : d0日目のコンテストとd1日目コンテストを交換してみる
            const int diff = randXor() % 10 + 1;    // d0とd1は10日差まで
            const int d0 = randXor() % (D - diff);
            const int d1 = d0 + diff;

サンプル2では、近傍1も近傍2も50%ずつの確率で選んでいますが、ここをどの近傍をどれぐらいの確率で試すかを調整すれば、性能を改善できるチャンスがあります。また、統計をとるのも大事です。遷移が成功した回数・失敗した回数のデータを取っておけば、どの近傍が有効なのかが分かり、問題を理解するヒントにもなります。さらに、「近傍1で遷移が成功すると、その直後で近傍2で遷移が成功しやすい」などの事実が分かれば、あらたに近傍3「近傍1のあとに近傍2」という新たな近傍を用意することもできるでしょう。

★★ Greedyに、次の状態を選ぶ。

先ほどの問題であれば、「仕事Aと仕事Bそれぞれから、常に作業時間が一番多くかかっている人を1人ずつ選び、交換」とGreedyに、次の状態を選ぶことができます。こういう選び方をすると、ベストスコアは序盤はどんどん伸びていきますが、局所最適に陥りやすいです。また、ありがちなのが、Greedyに選ぶアルゴリズムが、計算時間のボトルネックになってしまうパターンです。複雑なアルゴリズムより、ランダムでとにかくいろいろ試すのが焼きなまし法の強みです。Greedyにやるにせよ、多少ランダムを入れたり、計算時間はかからない単純な選び方をしたりする工夫が必要です。

★★ 序盤は大きく変化、終盤は小さく変化させたほうがいい。

単純にy=f(x)のyを最大化する問題なら、

序盤(t=0に近いとき) 次のx'は x'=x+rand()%1001 - 500
終盤(t=Tに近いとき) 次のx'は x'=x+rand()% 11 - 5

とか、
作業員割り当ての問題なら、

序盤(t=0に近いとき) 交換を100回やる
終盤(t=Tに近いとき) 交換を 1回やる

といったかんじです。スコアが局所最適でハマっている場合は有効です。ただ、焼きなまし法自体が、局所最適にはまりにくいアルゴリズムなので、あまり効果がない場合も多いです。

★★★★ 状態が大きく変化するわりには、スコアが変わらない近傍は良い。

2021/03/06 追加しました。

状態変化が大きいけど、スコアが大きい変化しかしない（悪化する確率が圧倒的に高い）
状態変化が小さいけど、スコアが小さい変化しかしない近傍

となりがちなのですが、問題によっては状態が大きく変化するわりには、スコアがあまり変化がしないケースがあります。こういう近傍があると、遷移が小さい近傍だけは辿りつけない状態にも短時間で行くことができ、焼きなましの性能がアップします。見逃さないようにしましょう。

★★★ 初期状態からすべての状態に行けるようにする。

2021/03/06 追加しました。
選んだ初期状態によっては、どんなに運がよくても用意した近傍ではすべての状態に辿りつけない場合があります。特に解に制約条件があるような問題（例：パズル問題など）で、このようなことが起こりやすいです。すべての状態にいけるような近傍を用意しましょう。

無理にランダムに大きく状態が変化するような近傍を入れてしまうと、それ自体が遷移の成功確率を大きく減らすことにもなり、全体の性能を落とす可能性があるので、簡単ではありません。
多点スタート（後述）にすれば、ある程度緩和されますが、多点スタートでは１つの解を求めるのにかけられる計算時間が減ってしまい、あまりよくありません。
スコア関数にペナルティ（後述）を入れる方法もあります。

★★ 良い初期状態からスタートする

これは問題に大きく依存する項目です。初期状態はてきとーでも良い場合と、すこし時間をかけて計算して良い状態から始めたほうが良い場合があります。特に、初期状態が悪いと状態を改善する近傍の選択肢が少なすぎる、逆に言えば、状態を改善すればするほどさらに改善できる可能性が増えるタイプの問題は、初期状態に少し時間を書けて求めて、それから焼きなましたほうが良い結果がでる場合があります。

3. スコア関数

スコア関数（scoring function）とも、評価関数（evaluation function）とも呼びます。

★★★★★ 良い状態を正しく評価できるような、スコア関数を新たに用意する

問題のスコア関数をそのまま使うと、焼きなまし法がうまく行かないことがあります。良い状態を正しく評価できるような、新たなスコア関数を用意しましょう。

[問題]
 （大きく略）…  i番目の人の満足値をs(i)とする。「満足度の最小値 min s(i) 」を、最大化しなさい。

この問題は「満足度の最小値 min s(i) 」を最大化する問題なので、素直に考えると、スコア＝「満足度の最小値 min s(i) 」としたくなりそうですが、これは良くありません。仮にそうした場合、

  状態A s(0)=  10, s(1)=10, s(2)=  10 のとき、スコアはmin{s(0),s(1),s(2)} = 10
  状態B s(0)=1000, s(1)=10, s(2)=1000 のとき、スコアはmin{s(0),s(1),s(2)} = 10

と状態Aと状態Bのスコアは同じになってしまいます。これはスコアは同じといえ、状態Bのほうが明らかに良い状態です。なぜなら、s(1)の点が仮に300点に増えたとしたら

  状態A' s(0)=  10, s(1)=300, s(2)=  10 のとき、スコアはmin{s(0),s(1),s(2)} =  10
  状態B' s(0)=1000, s(1)=300, s(2)=1000 のとき、スコアはmin{s(0),s(1),s(2)} = 300

と状態Bのほうは一気にスコアが増えます。しかし元のスコア関数のままだと状態Aと状態Bは同じスコアで、状態A→状態Bはスコア改善になりません。つまり焼きなまし法を行っても、状態A→状態Bには運が良くないと移動しません。
この問題であれば、例えば、
スコア＝1番小さいs(i) + 0.0001 * 2番目に小さいs(i)
とすれば

  状態A s(0)=  10, s(1)=10, s(2)=  10 のとき、スコアは 10 + 0.0001 *   10  = 10.001
  状態B s(0)=1000, s(1)=10, s(2)=1000 のとき、スコアは 10 + 0.0001 * 1000  = 10.1

と状態Bの方が好スコアになり、状態A→状態Bに移動しやすくなります。
ここは問題によって大きく有効かどうか大きく異なってきますが、必ず考慮に入れたほうがいいでしょう。結果に大差がつきやすいポイントです。

★★★スコアが改善しやすくなるようなスコア関数を決める。

上記の言い換えともいえるのですが、わりと焼きなまし法のスコア関数をつくるときに、問題のスコア関数をそのまま使ったり、違う状態を正しく評価しなかったりすると、同じスコアになりがちで、青い線のような飛び飛びの平坦な関数になることが多いです。赤いように、山登りしやすいスコア関数を作れないか考えましょう。必ずしも、問題のスコア関数の最大値と、焼きなまし法で使うスコア関数の最大値が一致する必要はありません。最大値をとりうるような状態（argmax）を一致させることが重要です。
f:id:shindannin:20150526014955p:plain

★★★スコア増分が0のときを、無くす。

2021/03/06 追加しました。
スコア増分が0のときは、焼きなまし法をやっても状態が行ったりきたりブラウン運動するだけで、解がなかなか改善しません。また、遷移するときの処理のほうが遷移しないときより重くなる場合、さらにひどいことになります。必ずスコア増分の履歴をチェックし、スコア増分が0になっているときはスコアの差をつけましょう。

★★★ 制約条件がある問題では、スコア関数にペナルティをつける。

2021/03/06 追加しました。
制約条件がある問題で、「制約条件を満たさない状態への遷移を許さない」とすると、ほとんど状態遷移されないままになってしまうことがあります。こういうときの対策としては、制約を満たしていない解も許して、ペナルティをつけて、スコア関数から減点します。

制約条件を満たしている度合いがひどいほど、ペナルティは大きく減点します。
計算の序盤ではペナルティは小さく、徐々にペナルティを大きくして、最後には絶対に制約条件を満たすようにします。
最後にでてきた最適解が制約条件を満たしているか確認しましょう（ただ、そうならないようなペナルティのつけ方を見つけるのが理想です。）

4. 遷移確率と温度

たいていの焼きなまし法の解説書には、expを使った方法が載っています。
焼きなまし法 - Wikipedia

遷移確率 P(e, e' , T) は e' < e の時に 1 を返すよう定義されている（すなわち下りの移動は必ず実行される）。
そうでない場合の確率はexp((e−e' )/T) と定義 

注：wikipediaの引用なので、本文の設定と違います。
    ここでのTは温度（=時間とともに減っていく値）です。
    最小化問題なのでe−e'となってます（最大化問題ならe'-eです）。

★時刻tに置ける温度Tを調整する

最初の例の以下のコードの部分です。

     const bool FORCE_NEXT = R*(T-t)>T*(rand()%R);

上の例だと、

t=0のとき、常にtrue
t=Tのとき、常にfalse

になるような線形関数にしています。だいたいの場合は、これで問題ありませんが、バリエーションはいろいろ考えられます。実際には、ベストスコアの更新状況をみて、更新があまりに序盤と終盤に固まっているときは、２乗してみるとか、ロジスティック曲線をつかうとか、その程度で良いと思います。

★★★★exp(e-e')/Tを使う。（e-e':スコアの悪化量）

wikipediaでは以下のように書いていますが、exp(e-e')/Tの形にしたほうが良いでしょう。（理由は、次回の改定時に書きます）

焼きなまし法 - Wikipedia

関数 P は e' −e の値が増大する際には確率を減らす値を返すように設定される。
つまり、ちょっとしたエネルギー上昇の向こうに極小がある可能性の方が、
どんどん上昇している場合よりも高いという考え方である。しかし、この条件は
必ずしも必須ではなく、上記の必須条件が満たされていればよい。

ただ、このexpの式、分子はスコア差なので分かりますが、分母の温度をどう決めれば良いかは分かりづらいです。~~目安としては、たまには許容しても良いスコアの悪化量を温度とすると良いです。~~ 最大の山を越えられるようにと考えると、考えられるスコアの最大値-最小値を初期温度を設定したほうが良いのですが、実際には温度調整して最終スコアがどうなるか実験してみてください。

double startTemp   =  100;
double endTemp     =   10;
double temp        = startTemp + (endTemp - startTemp) * t / T;
double probability = exp((nextScore - currentScore) / temp);  // 最大化なので、分子はnextScore - currentScoreで良い。
bool FORCE_NEXT    = probability > (double)(mXor.random() % R) / R;

時刻t=0（最初）でtemp=startTemp、時刻t=T（最後）でtemp=endTempとなります。

例えばスコアが100悪化したとき、nextScore - currentScore = -100なので、startTempを100にしてみます。endTempはとりあえず10にしてみましょう。
時間t=0であれば、exp(-100/100) = exp(- 1) = 0.36787944117と、3回に1回ぐらいは遷移します。
時間t=Tであれば、exp(-100/ 10) = exp(-10) = 0.00004539992と、まず遷移はしません。
このような感じでやると、良いと思います。

5. アレンジ

★★★★ 山登り

最初の例をFORCE_NEXT=0にすれば、山登り法になります。そもそも関数が凸であれば、山登り法も焼きなまし法も結果は一緒で、しかもrand()を使わない分、山登り法のほうが高速で、スコア改善のチャンスも多くなります。簡単に試せるので、試しましょう。

★ 多点スタート

焼きなまし法をつかっても、局所解にはまりやすい場合は、初期値を毎回かえた、多点スタートにする方法もあります。山登りと同時に使う方法もあります。ただ、多点スタートで結果がよくなるケースは、そもそもスコア関数や近傍が良くないので、そこを見直したほうがよいかもしれません。

★★★ 1変数ごとに焼きなまし

焼きなまし法で、たとえば、y = f(x1,x2,x3,x4,x5)と、状態変数が多いとき、次の状態のパターンが多くなり、結果的にあまり多くの状態を試せず、良い解が求められないときがあります。このような場合は、x2=x3=x4=x5を固定して、x1を焼きなまし、x1=x3=x4=x5を固定して、x2を焼きなまし、x1=x2=x4=x5を固定して、x3を焼きなましというふうに１変数ずつ焼きなまししていく方法があります。xの値がそれぞれ独立性が高い(?)場合は、この方法は有効です。

6. デバッグ

★ スコア差分の検算

2021/03/06 追加しました。
例えばサンプル2ではスコアの差分を計算していますが、いきなり書くとバグらせる可能性もあります。以下のような手順をとれば、バグがないか確認することができます。

サンプル1のgetFullScoreのように、全体のスコアの関数を用意して、それが正しいか確認します。通常のコンテストなら提出することで確認できます。
差分スコアrealDeltaScore = getFullScore(遷移後) - getFullScore(遷移前)として計算します。
サンプル2のようにdeltaScoreを直接求める方法ができたら、realDeltaScoreと一致するか確認します。

★ デバッグの際には、決定的にする

2021/03/06 追加しました。
状態やスコアが、まれにおかしくなるといったバグがあった場合、通常の焼きなまし法は非決定的なのでバグが再現ができない場合があります。そういったときは、デバッグ時には決定的にしましょう。

温度を求めるときにsystem clockを使わずに、最大ループ回数を固定して進行割合で温度を求めるようにしましょう。

    const static long long MAX_STEPS   =  10000000; // 終了までの回数
    for (long long steps = 0; steps < MAX_STEPS ; steps++) // 試行回数
    {
            const double progressRatio = static_cast<double>(steps) / MAX_STEPS;   // 進捗。開始時が0.0、終了時が1.0
            temp = START_TEMP + (END_TEMP - START_TEMP) * progressRatio;

乱数はシードさえ固定すれば決定的になるので問題ありません。
もしマルチスレッドを使っている場合は、グローバル変数とstatic変数に気をつけましょう。とくに乱数でstaticを使っている場合は乱数をクラス化するか、シングルスレッドで実行しましょう。

7. まだ書いていない内容

並列化
- 排他制御つきの焼きなまし
- ロックフリーの焼きなまし
タブーサーチ + 焼きなまし
レプリカ交換法

リンク集

基礎編

AtCoder wataさんによる公式解説
https://img.atcoder.jp/intro-heuristics/editorial.pdf

Tsukammoさんの記事
qiita.com

gacinさんの記事
gasin.hatenadiary.jp

応用編

ats5515さんは、巨大近傍法（状態遷移の回数は少なめになるけど、計算時間をかけてより良い次の状態を探す）が特に強いです。近傍の計算時間に。焼きなまし法の近傍を探すのに2段目の焼きなまし、制約条件をほぼ満たす準validな状態、温度遷移の工夫など、他の人があまり工夫しないもところでもいろいろバリエーションがあります。
ats5515.hatenablog.com

hakomoさんの記事は、まさに詳細という内容です。探索空間の話は、この記事が一番詳しいと思います。事例へのリンクも多いです。
github.com

2021-02-16

2021年2月の行動目標

今月も予定が読めないので、先月達成できなかった目標は簡単にしました。

競プロ（アルゴリズム）

高速フーリエ変換・数論変換の理解
ACLの遅延セグ木で10問解く
全方位木DPをライブラリ化

競プロ（マラソン）

Hash Codeの練習を5回する

将棋

実戦詰み筋事典を1周する（186問）

スポーツ

月10回リングフィットアドベンチャーをする。

概要

ChatGPTのいいなりになればOK

はまったところ

typescriptを使った設定にする必要があった。

リージョン間違いでログが何も見れなかった…

ジャッジ環境のディレクトリ構成が分からなかった。

別なバケット名を設定していた。

各種パスの更新をわすれていた

同時実行数が最大で10になっていた。

最後にChatGPTによるブログ

1. AWS CDKとLambda関数の作成

2. Step Functionsの構築

3. ログの確認

4. バケットとファイルパスの確認

5. 同時実行数の調整

本書の良い点

１．図が分かりやすい。

２．つまづきにくい。

３．ヒューリスティックスについて取り上げてある。

４．考察テクニックの章

５．コンテンツが充実

本書の賛否両論ありそうな点

コードの書き方

親切すぎる

同じジャンルでまとまっていて、必ずしも難度順にはなっていない。

難度と勉強時間の目安

おわりに

配列外アクセスをしたときの比較表

Visual Studio 2022で範囲外アクセスを気づきやすくする方法５つ

エラー一覧を「ビルド＋Intellisense」にする

sanitizerを積極的に使う

生配列よりstd::arrayがよい

Release版でSTLの範囲チェックしたいときは、 _CONTAINER_DEBUG_LEVEL=1 にする

インテリセンスが安定せず嫌な場合、clangを代わりに使うのがよい

はじめに

お金に関することについて

クレジットカード

Wise（旧 TransferWise）

租税条約や税務上の居住地に関する届け出

外国払い小切手は、日本のほとんどの銀行では換金できない

マネーロンダリングに対して厳しくなっている

口座閉鎖する意思があり、日本に戻ってくる前に口座が閉鎖できる状態であれば、現地にいる間に閉鎖してしまった方が良い

連絡方法について

インターネットバンキング

出国後、連絡手段別の問題点

日本にいる間にやっておいた方がよいこと

おわりに

はじめに

第１章 競技プログラミングは変質したのか？

短期コンテスト

1・打ち込むのが大変なアルゴリズムも出題されていてた。（減った）

2・バックスラッシュ（変化なし）

3・言語の選択（重要になった）

4・定数倍高速化（とんとん）

5・クイックソートのようなライブラリーが提供するアルゴリズムについての詳細（変化なし）

6・出題者の気持ちを読む能力（変化なし）

7. 枝刈り（減った）

長期コンテスト・最適化コンテスト

第２章 競技プログラミングは変質して、悪影響を与えたのか？

第３章 競技プログラミングをがんばっている皆さんへのアドバイス

なにかに熱中しているってこと自体が、素晴らしい。

競技プログラミングは役に立つ論

競技プログラミングを仕事に役立たせたい人が仕事に役立たせるためのコツ

競技プログラミングがおもしろすぎて、仕事を含む他の事に興味が持てない。

人生の目標が決まっていると、競技プログラミングをやる上でも迷わない。

Googleに入社したい方へ

付録１章 nuc氏の議論方法の問題点

[1] 自分の主張を読み取れないのは相手の責任にする。

[2] 相手の主張は自分の思いこみでより悪く解釈する。

[3] 分かりやすく書く気がない

[4] 不遜

その他

付録２章 nuc氏のグループは、競技プログラミングを生み出したのか？

付録３章 残る疑問

焼きなまし法の概要

サンプルソースコード

サンプル1

サンプル2

焼きなまし法のコツ

1. 高速化

第１章　競技プログラミングは変質したのか？

第２章　競技プログラミングは変質して、悪影響を与えたのか？

第３章　競技プログラミングをがんばっている皆さんへのアドバイス

付録１章　nuc氏の議論方法の問題点

付録３章　残る疑問