2014-03-29

C++11 forループの速度比較と、コンパイラのループ展開

C++ コンパイラ

C++11 forループの速度比較と、コンパイラのループ展開についてテストをしたときの結果です。構造体のメンバを、5で割った余りごとに分けて、頻度を数えるようなソースコードで実験しました（ソースコードは最後にあります）。プロセッサは、Intel(R) Core(TM) i7-3632QM CPU @ 2.20GHzですが、実行結果は、コンパイラ・CPU・メモリ・キャッシュで大きく異ってくると思うので、ざっくりとだけ参考にしてもらえればと思います。

1. ループの方法ごとの速度の比較

Visual Studio 2012は、Release、その他は初期設定のままでコンパイルしました。
g++ 4.8.2は、--std=c++0x -O2 -W -Wall -Wno-sign-compareでコンパイルしました。

方法	Visual Studio 2012（秒）	g++ 4.8.2（秒）
(1) 通常のforループ	2.995	3.562
(2) 通常のforループとconst参照	3.035	3.579
(3) c++11のrange-based forループ	3.604	3.502
(4) for_eachとc++11のラムダ式	3.619	3.462
(5) for_eachと関数オブジェクト	3.604	3.477

Visual Studio 2012で(1)(2)が速いのは、ループ展開が行われているからです。g++ 4.8.2は、(1)から(5)までおおよそ同じ時間です。デフォルトのオプションでは、ループ展開しないようです。
(4)と(5)は、http://msdn.microsoft.com/ja-jp/library/dd293608.aspx にあるように、C++11のラムダ式は関数オブジェクトを使用したものと同じになります。実際に、Visual Studio 2012でコンパイルすると、DebugでもReleaseでも(4)と(5)は、全く同じアセンブリになりました。

2. コンパイラのループ展開の仕方

（同じコードを使いましたが、ちょっと前に違う状態で実験したので、当時の簡易的な実験の結果として見てもらえれば）

ループ展開とは、コンパイラの高速化の手法です。

for (int i = 0; i < 10000; ++i)
{
	frequency[positions[i].x%SZ(frequency)]++;
}

上のようなコードを、下のようなコードに置き換えて、ループ回数を減らします。（動作はかわりません）

for (int i = 0; i < 10000/5; ++i)
{
	frequency[positions[i*5].x%SZ(frequency)]++;
	frequency[positions[i*5+1].x%SZ(frequency)]++;
	frequency[positions[i*5+2].x%SZ(frequency)]++;
	frequency[positions[i*5+3].x%SZ(frequency)]++;
	frequency[positions[i*5+4].x%SZ(frequency)]++;
}

メリット・デメリットについて、詳細はこちらのリンクを参考にしてみてください→ http://ja.wikipedia.org/wiki/%E3%83%AB%E3%83%BC%E3%83%97%E5%B1%95%E9%96%8B

Visual Studio 2012

Nを定数にした場合、6以下の約数で最も大きい個数に展開するようです。Nが素数のときや、2でしか割り切れないときは遅くなりました。

N	ループ展開の個数	実行時間（秒）
9996	4	2.839
9997	1	3.213
9998	2	3.136
9999	3	2.854
10000	5	2.871
10001	1	3.276
10002	6	2.855
10003	1	3.214

Nを変数にした場合（標準入力でNに値を渡した場合）は、ループ展開はされませんでした。

g++ 4.8.2

Nを定数にした場合、コンパイルオプションに-funroll-loopsを追加すると、ループ展開されます。12個までループされる展開を確認できましたが、8個や12個まで展開されたときは、かえって遅くなりました。
Nを変数にした場合（標準入力でNに値を渡した場合）は、 -funroll-all-loopsを追加すると、ループ展開されます。この場合、8個にループ展開されましたが、Nが8で割り切れないことを考えて、ループを途中で抜けるジャンプ命令が入ってしまうため、かえって遅くなってしまいます。

ソースコードです。

#include <vector>
#include <algorithm>
#include <iomanip>
#include <iostream>
#include <fstream>

using namespace std;
typedef long long ll;
#define SZ(a) ((int)a.size()) 

#include <sys/time.h>
unsigned long long getTime() {
	struct timeval tv;
	gettimeofday(&tv, NULL);
	unsigned long long  result =  tv.tv_sec * 1000LL + tv.tv_usec / 1000LL;
	return result;
}

struct POS
{
	int x;
	int y;
};


class FunctorClass
{
public:
	explicit FunctorClass(vector <int>& frequency) 
		: m_frequency(frequency)
	{
	}

	void operator()(const POS& pos) const
	{
		m_frequency[pos.x%SZ(m_frequency)]++;
	}

private:
	FunctorClass& operator=(const FunctorClass&);
	vector <int>& m_frequency;
};



int main()
{
	int N = 10000;
	vector <POS> positions(N);
	for (int i = 0; i < N; ++i)
	{
		positions[i].x = rand();
		positions[i].y = rand();
	}

	const int DIVIDE = 5;
	vector <int> frequency(DIVIDE);

	const ll start = getTime();

	for(int k = 0; k < 100000; ++k)
	{
#if 1
		// (1) 通常のforループ
		for (int i = 0; i < N; ++i)
		{
			frequency[positions[i].x%SZ(frequency)]++;
		}
#elif 0
		// (2) 通常のforループとconst参照
		for (int i = 0; i < N; ++i)
		{
			const POS& p = positions[i];
			frequency[p.x%SZ(frequency)]++;
		}
#elif 0
		// (3) c++11のrange-based forループ
		for (const POS& p : positions)
		{
			frequency[p.x%SZ(frequency)]++;
		}
#elif 0
		// (4) for_eachとc++11のラムダ式
		for_each(positions.begin(),positions.end(), [&frequency] (const POS& pos) {
			frequency[pos.x%SZ(frequency)]++;
		});
#else
		// (5) for_eachと関数オブジェクト
		for_each(positions.begin(),positions.end(), FunctorClass(frequency));
#endif
	}

	cout << " Time=" << getTime()-start << endl;

	for (int i = 0; i < SZ(frequency); ++i)
	{
		cout << " frequency[" << i << "]=" << frequency[i] << endl;
	}

	return 0;
}

2014-03-01

混合ガウス分布のEMアルゴリズム、C++実装例（2次元のみ）

TopCoder マラソンマッチ機械学習

f:id:shindannin:20140301205110p:plain

先日のTopCoderマラソンマッチ「Octave Classifier（カテゴリー分けする機械学習系の問題）」で、使わずじまいに終わったC++のコードをアップします。

混合ガウス分布のEMアルゴリズムについて、全く知らなかったので、

EM アルゴリズム実装(勉強用) - Mi manca qualche giovedi`? Nakatani Shuyoさん
混合モデルとEMアルゴリズム山中高夫さん
PRML本第9章

を参考にしました。ありがとうございます。基本的に、Nakatani Shuyoさんのコードの移植ですので、比較すると分かりやすいかもしれません。ただ数学関数は自前になってます。2次元限定ですので、ご了承ください。

Rやpython等で実装している方が既にいるので、C++での需要はないかもしれませんが、

型が分かりやすい
ライブラリがなくても、単独で動く。

というメリットはあるので、もしかしたら少しは参考になるかもしれません。

実際にideone.comで実行した結果はhttps://ideone.com/LXH8viです。入力データセットは、Rに付属しているfaithfulというものです（Nakatani Shuyoさんのページと同じです）。3クラスで実行しました。ideoneの出力データをそのままRでplotしたものが、最初の画像になります。どうみても2クラスに分けるためのデータセットですが、テストということで。

#include <iostream>
#include <vector>
#include <cassert>
#include <cmath>
#include <numeric>
#include <stdio.h>
#include <stdlib.h>

using namespace std;
#define SZ(a) ((int)((a).size()))

// 注：データの次元D=2のときしか対応していません！
typedef vector <double> Vec;
typedef vector <Vec> Mtx;

class EMGaussianMixtures
{
private:
	int N; // データ個数
	int D; // データの次元
	int K; // クラスの種類数
	Mtx	m_xx;				// ｘ：正規化したデータ m_xx[N][D]
	Mtx	m_mu;				// μ：平均             m_mu[K][D]
	Vec	m_mix;				// π：混合率           m_mix[K]
	vector < Mtx >	m_sig;	// Σ：共分散           m_sig[K][D][D]
	Mtx	m_gamma_nk;			// γ：負担率			m_gamma_nk[N][K]

public:

	// 初期化
	// データセット		dataFrame[N][D]
	// クラスの種類数	numClasses -> K
	void initialize(const Mtx& dataFrame, int numClasses)
	{
		N = SZ(dataFrame);
		D = SZ(dataFrame[0]);
		K = numClasses;
		assert(N>=1);
		assert(D==2);
		assert(K>=1);

		// データの正規化
		m_xx = dataFrame;
		normalize(m_xx);

		// 平均、共分散、混合率の初期値(正規乱数)
		m_mu	= Mtx(K, Vec(D));

		for(int row=0;row<K;++row)
		{
			for(int col=0;col<D;++col)
			{
				m_mu[row][col]= getNormRand(); // たぶん、必須ではないけど、元のコードに合わせました。
			}
		}

		m_mix = Vec(K, 1.0/K);

		m_sig = vector < Mtx >(K, Mtx(D, Vec(D)));
		for (int k = 0; k < K; ++k)
		{
			for (int rc=0; rc<D; ++rc)
			{
				m_sig[k][rc][rc]=1.0;
			}
		}
	}

	// E stepとM stepを1回ずつ実行
	void run()
	{
		m_gamma_nk = calcEstep(m_xx, m_mu, m_mix, m_sig);

		Mtx	new_mu;
		Vec new_mix;
		vector < Mtx > new_sig;

		calcMstep(new_mu, new_mix, new_sig, m_xx, m_gamma_nk);

		m_mu = new_mu;
		m_mix = new_mix;
		m_sig = new_sig;
	}

	void printGammaNK() const
	{
		for(int n=0;n<N;n++)
		{
			for(int k=0;k<K;k++)
			{
				printf("%.10f",m_gamma_nk[n][k]);
				if(k<K-1)
				{
					printf(", ");
				}
			}
			printf("\n");
		}
	}

private:
	// 正規化。平均0、不偏標準偏差1にする。
	void normalize( Mtx& xx ) const
	{
		for (int col=0;col<D;++col)
		{
			double mean = 0.0;	// 平均
			for (int row=0;row<N;++row)
			{
				mean += xx[row][col];
			}
			mean /= N;

			double sd	= 0.0;	// 不偏標準偏差
			for (int row=0;row<N;++row)
			{
				const double diff = xx[row][col]-mean;
				sd += diff * diff;
			}
			sd	/= (N-1);	// 標準偏差じゃなくて不偏標準偏差なので、NじゃなくてN-1で割るのに注意。
			sd	= sqrt(sd);

			// 平均を引いた後に、不偏標準偏差で割る。
			for (int row=0;row<N;++row)
			{
				xx[row][col] = (xx[row][col]-mean)/sd;
			}
		}
	}

	// 行列と行列の積
	inline Mtx mul(const Mtx& a, const Mtx& b) const
	{
		vector <vector <double> > c(SZ(a), vector<double>(SZ(b[0])));
		for (int i = 0; i < SZ(a); i++)
		{
			for (int k = 0; k < SZ(b); k++)
			{
				for (int j = 0; j < SZ(b[0]); j++)
				{
					c[i][j] += a[i][k]*b[k][j];
				}
			}
		}
		return c;
	}

	// スカラーと行列の積
	inline Mtx mulScalar(const Mtx& a, const double scalar) const
	{
		Mtx ret(a);
		for (int i = 0; i < SZ(ret); i++)
		{
			for (int k = 0; k < SZ(ret[0]); k++)
			{
				ret[i][k] *= scalar;
			}
		}
		return ret;
	}

	// スカラーとベクトルの積
	inline Vec mulScalar(const Vec& a, const double scalar) const
	{
		Vec ret(a);
		for (int i = 0; i < SZ(ret); i++)
		{
			ret[i] *= scalar;
		}
		return ret;
	}

	// 行列の転置
	inline Mtx transpose( const Mtx& vs ) const
	{
		const int H = SZ(vs);
		const int W = SZ(vs[0]);

		Mtx ret(W, Vec(H) );
		for (int y = 0; y < W; y++)
		{
			for (int x = 0; x < H; x++)
			{
				ret[y][x] = vs[x][y];
			}
		}

		return ret;
	}

	// 2*2の行列式を求める
	inline double det(const Mtx& m) const
	{
		return m[0][0]*m[1][1]-m[0][1]*m[1][0];
	}

	// 2*2の逆行列を求める
	inline Mtx solve(const Mtx& m ) const
	{
		vector < vector <double> > ret(m);
		swap(ret[0][0],ret[1][1]);
		ret[0][1] = -ret[0][1];
		ret[1][0] = -ret[1][0];
		ret = mulScalar(ret,1.0/abs(det(m)));
		return ret;
	}

	// 多次元正規分布密度関数を求める
	double getDMNorm(const Vec& x, const Vec& mu, const Mtx& sig) const
	{
		Vec x_mu(x);	// x - mu
		for (int i = 0; i < SZ(x_mu); i++)
		{
			x_mu[i] -= mu[i];
		}

		const Mtx inv = solve(sig);

		// D=2決め打ちなので、mul(mul(transpose(x_mu),solve(sig)),x_mu)の部分を展開し、Cとした。
		const double C = x_mu[0]*(x_mu[0]*inv[0][0]+x_mu[1]*inv[1][0]) + x_mu[1]*(x_mu[0]*inv[0][1]+x_mu[1]*inv[1][1]);

		double ret = 1/(sqrt(pow(2.0*M_PI,D) * det(sig))) * exp( -0.5 * C );

		return ret;
	}

	// Eステップ。返り値は gamma_nk[N][K]
	Mtx calcEstep( const Mtx& xx, const Mtx& mu, const Vec& mix, const vector < Mtx >& sig) const
	{
		Mtx ret;

		for(int row=0;row<N;++row)
		{
			Vec numer(K);
			for(int k=0;k<K;k++)
			{
				numer[k]=mix[k]*getDMNorm(xx[row], mu[k], sig[k]);
			}
			const double sum_numer = accumulate(numer.begin(),numer.end(),0.0);

			for (int k=0; k < K; k++)
			{
				numer[k]/=sum_numer;
			}

			ret.push_back(numer);
		}

		return ret;
	}

	// Mステップ。次のステップのmu,mix,sigを求める。
	void calcMstep(	Mtx& new_mu, Vec& new_mix, vector < Mtx >& new_sig, const Mtx& xx, const Mtx& gamma_nk) const	
	{
		new_mu.clear();
		new_mix.clear();
		new_sig.clear();

		Vec N_k(K);
		for(int n=0;n<N;n++)
		{
			for (int k = 0; k < K; k++)
			{
				N_k[k] += gamma_nk[n][k];
			}
		}

		new_mix = N_k;
		for (int k = 0; k < K; k++)
		{
			new_mix[k] /= N;
		}

		new_mu = mul(transpose(gamma_nk),xx);
		for (int k = 0; k < K; k++)
		{
			new_mu[k] = mulScalar(new_mu[k], 1.0/N_k[k]);
		}

		new_sig = vector < Mtx >(K, Mtx(D, Vec(D)));
		for(int k=0;k<K;++k)
		{
			for(int n=0;n<N;++n)
			{
				Vec x_newmu(xx[n]);	// x - new_mu
				for (int i = 0; i < SZ(x_newmu); i++)
				{
					x_newmu[i] -= new_mu[k][i];
				}

				// D=2きめうち
				new_sig[k][0][0] += gamma_nk[n][k] * x_newmu[0] * x_newmu[0];
				new_sig[k][0][1] += gamma_nk[n][k] * x_newmu[0] * x_newmu[1];
				new_sig[k][1][0] += gamma_nk[n][k] * x_newmu[1] * x_newmu[0];
				new_sig[k][1][1] += gamma_nk[n][k] * x_newmu[1] * x_newmu[1];
			}

			new_sig[k] = mulScalar(new_sig[k], 1.0/ N_k[k]);
		}
	}

	// おおよその標準正規乱数（平均0、分散1）
	double getNormRand() const
	{
		double ret = 0.0;
		for( int i = 0; i < 12;i++ ){
			ret += (double)rand()/RAND_MAX;
		}
		return ret-6.0;
	}
};

int main()
{
	EMGaussianMixtures	*em = new EMGaussianMixtures();

	// 入力
	Mtx dataFrame;
	Vec pos(2);
	while (scanf("%lf %lf",&pos[0],&pos[1])!=EOF)
	{
		dataFrame.push_back(pos);
	}

	// 初期化
	const int numLoops	 = 20;
	const int numClasses =  3;
	em->initialize(dataFrame, numClasses);

	// 実行
	for (int i = 0; i < numLoops; i++)
	{
		em->run();
	}

	// 出力
	em->printGammaNK();

	delete em;

	return 0;
}

2014-03-01

TopCoder Marathon Match（機械学習・データマイニングもあるよ）

TopCoder マラソンマッチ機械学習

(2012年12月16日の記事を、Qiitaから移行したものです。)

Machine Learning Advent Calendar 12/16の記事です。主催のnaoya_tさん、有難うございます。今回は、機械学習やデータマイニングを実際楽しみながら使えるTopCoder Marathon Matchの紹介をしようと思います。

TopCoder Marathon Matchとは

TopCoder (http://community.topcoder.com/tc) は、インターネット上で、世界の人とプログラミングなどで競い合うコミュニティです。TopCoderというと、75分間でアルゴリズムに関するプログラミングを作れるかで対決する、Algorithm Single Round Matchが有名なのですが、他にもMarathon Matchというのがあります。Marathon Matchは、長期間で行われ、問題は多岐にわたり、機械学習やデータマイニングを題材にした問題が出題されることがあります。

Marathon Matchの基本ルール

（マッチによって、ルールが異なることもあります。）

問題は英語で出題されます。

使える言語・ライブラリ

- オンライン（提出し実行する）使える言語は、C++、Java、C#、Visual Basic、Pythonです。外部のライブラリもライセンスの種類によっては使えます。
- オフラインで行う機械学習用には、何の言語を使っても構いません。
- オンラインではメモリ・コードのサイズ・計算時間に制限があります。マッチによって異なります。

スコア関数というのがあります。結果の良さを表すスコアを求められます。例えば、(実際の値 - 予測値)の差が小さいほど高得点といったかんじです。スコア＝「出題者側が最も重視するところ」といえ、このスコアが高い方が優勝となります。

TopCoderの登録方法

http://community.topcoder.com/tc のページ右上の"Register Now"から登録できます。登録の方法はpokutuna氏のページが分かりやすいと思います。 http://pokutuna.hatenablog.com/entry/20080720/1216514672

参加方法

1. イベントカレンダーで、開催日を確認します。 http://community.topcoder.com/tc?module=Static&d1=calendar&d2=thisMonth （Events -> Event Calendarで行けます）
マラソンマッチは突然現れることが最近は多いです。TopCoderのトップページや、送られてくるメールでも、開催の確認をすることができます。

2. マラソンマッチが開催されたら、登録します。Algorithm -> Marathon Match -> Active Contestsで行けます。 http://community.topcoder.com/longcontest/?module=ViewActiveContests
今は開催されているコンテストがないですが、あるときは問題が現れるのでregisterボタンを押して登録します。

3. 自分の解答ができたら、submitボタンを押して提出します。自分のコードと、Test ExampleとSubmitの2種類のボタンが現れます。
- Test Exampleは、少ないケースでの結果を知ることができます。
- Submitが本提出になります。より多くのケースでの結果と、仮順位も知ることができます。

4. コンテストが終わると、より多いケースでスコアが求められます。数日で、最終結果がでます。

どんなコンテストがあるのか？

2012年にあったマラソンマッチです。データマイニング系の問題は以下のとおりです。

USPTO Algorithm Challenge

米国特許商標局の主催マッチ。特許の図の画像と特許の文書とを解析して、書かれている番号を自動的に取得するプログラムを書く問題です。トレーニングデータも用意されてます。画像処理（文字認識）と文書解析の、機械学習の総合的能力が問われる問題でした。ランダムで2人組のチームを組むという変わったルールで行われました。

NASA NTL Marathon Match 1 VehicleRecognition

NASAが主催のマッチ。衛星写真で車かどうかを判別する問題でした。完全に画像処理の問題。日本人参加者のmsiroさんがSVMを使って優勝しました。msiroさんのブログはこちら http://msirocoder.blog35.fc2.com/blog-entry-67.html

Soybean Marathon Match

大豆の種別や畑などのトレーニングデータから、大豆の良しあしを判別する判別分析の問題や、収穫量を与える回帰分析っぽい問題が出題されました。

Soteria Serious Injury Prediction

保険会社からの出題。職場に関するさまざまなデータから、今年の職場でケガが起きる件数を予測する問題です。SVMや決定木っぽい解法が上位に多かったのですが、優勝した方は、とても単純な回帰式（2年前の職場のケガ数でほとんど決まる）で、優勝しました。

HMS Challenge #1 MinorityVariants

ハーバード大学メディカルスクールからの出題。遺伝子のデータの読み間違いを、判別する問題。機械学習が力が発揮できそうな問題でしたが、実際にはある遺伝子に関する情報に、重要な法則性があることがあり、ほぼ100%当てれるという結果に…。

データマイニング以外にも、GPGPUを使った問題、本当に数学的な難問、圧縮解凍の問題、パズル系の問題、完成しているコードを高速化させる問題など、問題は種類は多岐にわたります。

全体的な流れ

文章だけ書いても伝わらないと思うので、全体的な流れだけを、とてもざっくりと。

HMS Challenge #4 BostonRiskPrediction

ハーバード大学メディカルスクールからの出題。ボストン市内の住人データ・地理データ・2011年の1月～8月までの緊急コールのデータなどが与えられるので、そこから2011年9月～12月の間に、何月何日に、どこで、何件緊急コールがかかってくるかを予測する問題です。

ボストン市内の膨大なデータがトレーニングデータとして与えられます。これは地域別の人種割合データ・土地の値段・場所などのグラフです。

実際に1月～8月まで緊急コールが去年かかってきた場所をプロットしたもの。20万件近くかかってきていて、ボストン市内の形がそのままでてます。実際のデータなので、本格的ですが、たまに誤入力もあり、データクレンジングも必要です。

コードを書いて提出します。自分の場合はVisual Studioでコードを書いて、ブラウザ上に提出しています。Submissionを押すと本提出です。

仮のスコアと順位ができます。Marathon Matchの過去の戦績によりレーティングがつくので燃えます。特に赤い色のはレッドコーダーと呼ばれ、恐ろしく強いです。

こんなのの繰り返しで、最終日まで競います。

参加するメリット

実際に、自分が行っているがデータマイニングや機械学習の手法が有効なのか、世界の人との競争で確かめることができます。

マッチ終了後に、他の人のコードが見れます。同じ問題でも、いろいろなアプローチがみられます。時には機械学習を使ってないベタな手法が勝つこともあり、逆に機械学習が圧勝することもあります。どちらの場合もとても勉強になります。

成績上位だと、賞金がでます。1位だと$5000、5位でも$500ぐらいもらえます。まだまだデータマイニング系のマッチは、他のTopCoderの部門と比べるとレベルが高いとはいえないので、チャンスです！

というわけで、機械学習を作ったり使ったりしてる方で、気になった方は、ぜひ参加してみてください！

2014-03-01

Marathon Match 74

TopCoder マラソンマッチ

(2011年10月29日の記事を移行したものです。)

マラソンスタートしました(10/29)

前回の反省を生かして、文章化することにしました。

ファーストインプレッション(10/29)

Anti..巡回セールスマン問題の最長路を求める問題かな？（注：間違いです！）
- 初期の点が何個かあるといえ、これって研究している人がいそうで、めっちゃ不利なネタな気がする…。
- ２次元の巡回セールスマン問題って、ETSP(Euclidean (Euclidian) traveling salesman problem)というんですね。
- 検索してみた。
  - http://www-or.amp.i.kyoto-u.ac.jp/algo-eng/db/demo/TSP/index.html
    - 最短路は線が交差しないようなので、最長路を目指すなら線が交差するといい？
  - http://maven.smith.edu/~orourke/TOPP/P49.html
    - showed that the maximum TSP can be solved in time O(n) for rectilinear distances in the plane 2次元の最長TSPはO(n)で解ける！なんと論文があるとは… （注：これはrectlinear distanceです。euclid distanceではありませんので、実は全然違う）
    - いや、でも、これぐらいは作題者が気づくんじゃないか。テスターもTCOファイナリストだし。
    - 問題を読み直してみる。
    - 誤読してましたorz

問題
2次元巡回セールスマン問題。2次元平面に都市が何個かある。セールスマンは、スタートの都市から、すべての都市を１回ずつ訪問して、スタートの都市に戻ってきたい。普通の巡回セールスマン問題とは違い、このセールスマンは、まだ訪れていない都市の中でもっとも近い都市を訪れる（最短経路を通るアルゴリズムではない）。あなたは追加で都市をN個置ける。セールスマンの移動距離が最大になるように、都市を置きなさい。

Nはpower(10,X) Xは1.0～4.0まで均等。つまりN=10～100まで1/3,N=100～1000まで1/3,N=1000～10000まで1/3。
元から配置されてる都市は3～min(10,N/3)
- ほとんどのケースで3～10ってこと？かなり少ない印象。大きく影響を与えるんだろうか…
相対スコア。得点は(あなたの距離/1位の人の距離)の4乗！
- これは、ちょっとの距離差でも大きく点差が開きそう。前回の反省を生かして、Nにあわせて、きめ細かくやる。
計算時間は10秒！。今回は間違えない！

要するに、いまいちなアルゴリズムで動くサラリーマンを、わざとたくさん歩かせるように都市をおく問題。
- いや、いまいちか？２次元平面上なら、単に一番近い都市をどんどん訪れるというのは、かなり最適解に近くなりそうだが。このアルゴリズムの弱点を突かねばなるまい。
焼きなまし系のアルゴリズムは使えるんだろうか？計算量的にはいけそうだけど…。というよりは幾何の問題？
1000000000*1000000000のフィールドをそのまま使うのがいいのか、量子化したほうがいい？
点を何個かのグループに分ける。ただ、分けたグループの最適解は、全体の最適解とはぜんぜん近くならなそうな気もする。
長時間計算すればするほど、結果がよくなるタイプの問題なんだろうか？もし、そうであれば長時間計算して求めた解の性質を探したいところ。
問題を勘違いしたものの、ETSP　max ETSPの解放はチェックしたほうがいいかも。ちょっと役に立つこともあるかも。
単に格子点に都市をおいたら結構強い？

アプローチ1 じょじょに移動距離を増やしていく

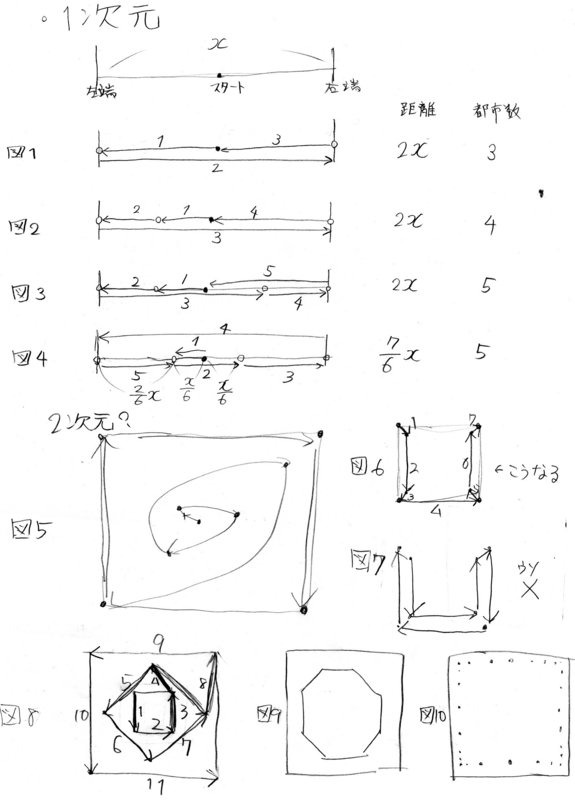
まずは１次元で考えてみる。図1のように、点はまず端においたほうが距離が伸びる。ただ図3に注目。端に置いた後、真ん中に置くのは正しくない。できるだけいったりきたりするようにさせるためには、図4のように最初に動きすぎてはいけないことが分かる。
これを２次元に応用すると、図5のような形になるのかなぁ…。じょじょに移動距離が長くなっていき、２次元に展開にするには、こんなかんじかと。ただし、図6・図7のように、このうずまきの距離を大きくするために、うずまき間の距離を狭くしてしまうと、セールスマンが最短距離のところに移動してしまうため、うずまきにならない。
図8は結構よさそう。つまり、うずまきを作る多角形の辺の長さと、うずまき間の頂点距離を同じにする。図8だと1,2,3,4が等距離、5,6,7,8が等距離になっている。１辺の長さをxとすると、かなり少ない点の数で8x(=4x+2x+x+0.5x...)ぐらいまでの長さが作れそう。
ただし若干端が無駄な気がするので、図9のような正多角形もあるかもしれない。いろんな形を試そう
また図10のように等間隔でなくても、ある程度いけるのかも…
いろんな幾何図形を考えてみよう。ネットで探したり、街中でものを注意してみたり、画像検索もありかもしれない。

アプローチ2 行き止まりに追い込み交差させる。

線が交差するのは、距離が伸びるので基本的によいこと。また、等間隔に点をおけば、セールスマンの移動方向をコントロールできる（今回の問題で距離が同じ点の場合は、IDの小さいほう優先とあるので、IDはこちらで勝手に決められるので実質コントロール可能）。なのでうまく行き止まりに追い込めば、無駄に移動させることができるはず。
これも等間隔というのさえ守れば、いろんな図形が考えられるかもしれない。四角形・三角形は確かに充填率は高そうだけど。
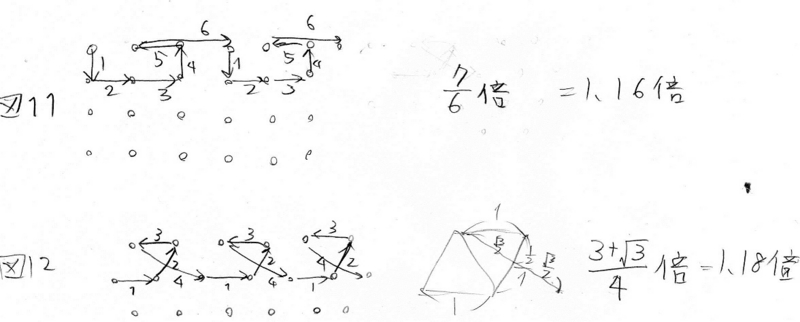
図11は四角形でおいた場合。思いつく限りでは、この例が行き止まりに持ち込めやすそう。ただ、行き止まり頻度が少なくても、行き止まりの脱出距離が長ければお得になるので、それは検討しないと。
図12は三角形でおいた場合。1.18倍とわずかながら上。あと、こちらのほうが、同じ点の数でも図11より１辺の長さを大きくできそう。ただ、今回整数の座標にしか点がおけないのが、ちょっときついかも。
この思いついた2とおりだけでは、距離がいまいち伸びてない。ここは、BitDPでメモ化探索をして、試すのがよさそう。自分では尾もいつかなそうなので。計算時間がかかりそうなので、早めに仕掛けておく。

終了(11/8)

結局、実装に夢中になっていて、終わってしまった…。
まずは放送用にメモのみ。

10/30 submission 1 単にグリッド上におくだけ15点ぐらい

じっさいに書いてみると、スカスカの部分が多いので、別の形に変更。
うしろからGreedy submission 2 40点。2時間ぐらいなので、意外と高得点。
方針決定

斜め移動の階層

うしろからGreedy

四角移動の階層
- 各エリアをどう通過するか、ハミルトン路を決める
- それぞれのエリア内でビットDPをする

土曜ハミルトン路、どうやってもとめるの?
39$バカ
結局、自力で求められたけど。
日曜
- 実装、難しいとは思ってたけど予想以上に難しい
- 斜め移動→四角移動の階層へ移動するときに、
-
日曜深夜
- 実装なんとかできたが低スコア
- 原因:荒過ぎる。いろいろな階層数をためしたとしても、使用している点の数が、Nと離れていて、その分スコアを失う。
- 対策1:足りない点は、他のメッシュで埋める。
  - 点が増えるが、前提が崩壊して点があまり伸びないケースあり。
  - しかも、座標の扱いに大きく失敗しているので、実装難。
- 対策2:多すぎる点はまびきする。
  - 間引きできるパターンは限られる。あまり点が伸びない
月曜朝わるあがき
- ビューワで点をてきとうにドラッグ。「うしろからGreedy」から点が増えてるんですけど…
- てきとーに山登りしてみる。submission 59点。休み3日以上使ったのに、てきとーな解のほうが圧倒的によい。

反省点

最初は、広く浅く！
座標の扱い方。
- 2,3,4,5でたくさん割り切れる数字でやっとけば。27000の倍数とか。
- 最初から決めうちは、あとで間違いにきづくときつい。
長時間焼きなまししておいて、解を予想するという方法もあったのでは？特に、自分の頭だけで考えている時間、コンピューターにも考えさせよう。

他の方の解法

後ろから、うそDP
ある点からもっとも近い点の判定。四分木・x軸のみソートとか

2014-03-01

Marathon Match 72

TopCoder マラソンマッチ

(2011年7月22日の記事を移行したものです。)

結果

7位/44 Rating 1694→1783
裏マッチだったので、強いのはcolunさんだけなのに、7位。結果のわりには、レートは上がったのは、たまたま自分より上の順位の人が新規の方ばかりだったから。結果を反省せねばなりません…。

問題

平文を圧縮してください。平文の文字列長は500ぐらい～100000。圧縮後の文字列の長さ（辞書みたいなかんじ）も決められてます。例えば、以下のようなかんじに圧縮してください。

S[1] = bpa4h2edn2b3k2d3z2e43b
S[2] = 3i3ufx4uku34gzfob4vlozd3m
S[3] = juquvqvrudlpqezzzchprdwi
S[4] = kozid3pvevaytgjxdmjpfbsfhxrtovqp

暗号の解凍アルゴリズムは決まってます。数字の部分xは、番号のS[x]の文字列に置き換えられます。解凍後の文字列が、元の文字列と同じであればあるほど高得点。その他、もとの平文はランダムで文字が置き換わる確率はテストケースで大きく異なります。
すごくざっくり言うと、「覚えられる単語数が極端に少ない辞書式圧縮で、劣化をできるだけ抑えよ」という問題です。

反省点

放送中に、chokudaiさん、yowaさんから頂いたアドバイスなどを元に反省。

日記を書きながらやろう
- 自分の考えが整理できます。
- 最初のほうに思いついたアイディアを後で使いたくなったときにも使えます。
- あとで日記を思い出しながら書く時間もはぶける（時間たってからの復習は、ものすごく時間がかかる）
幅優先探索のメリット
- 今回の問題は、深さ優先探索よりも幅優先探索のほうが有利。この問題では、「最初の単語を当てはめを間違うと、そのあとは全然ダメである。さっさと打ち切りたい。」　これに深さ優先探索を使ってしまうと、最初の単語の当てはめ方が良かったのかイマイチだったのかが分からないまま、どんどん深い方へ探索してします。幅優先探索であれば、他の候補と相対的に良い悪いを比較できます。最初の単語の当てはめ方が一番良かったものに、より多くの探索時間をかけるといったことも可能です。
問題をよくよめ
- 時間制限は毎回違います。今回は10秒と誤解してしまいましたが、本当は30秒でした。よく読みましょう。
- 今回は数字の使われ方を理解してませんでした（必ず1種類につき1個～4個使われる）。普通のAlgorithmマッチでは、細かい条件も使える場合がとても多いので、よく読みましょう。
Marathonスコアが低い場合は、いいアイディアが思いついていないのではなく、基本的なアイディアに気づいていないだけ。
- 一見いいアイディアがでてないようにみえますが、結果をみてみると大抵の人が思いつきそうなものをボロボロと落としていました。今回の問題もビューワを書いたほうがよかったかもしれません。
きめ細かくやる
- 神頼みフェーズ手抜きすぎました。裏マッチでも意外とちゃんとやっている人が多かったです。特に相対スコアルールのとき、こういうところで点を落としやすいので気をつけましょう。

方針

ボトムアップで、短い単語から、平文から数字に置き換えていく。
トップダウンで、長い単語から、平文から数字に置き換えていく。（最終的に企画倒れ）
神頼みフェーズ（一番使われているのが多い文字で埋める）

ボトムアップで、短い単語から、平文から数字に置き換えていく。

S[x]の同じ長さの部分文字列の中で、たくさんでてくる「似たような」文字列を探す。探し方は以下の通り。
- （このやり方より、「一番短い部分文字列は、必ず最初の32文字以内に現れる」の法則を使ったほうが、確実かつ高速だったと思います。全く気づけませんでした。ビューワ作ってれば気づいてたかも…）

例えば、"ABCDEFABXDE"の中にある似たような部分文字列（長さ5）を知りたいとき
(1)連続する2文字のハッシュ値の登場回数をカウント
map[連続する2文字のハッシュ]++
AB 2点
BC 1点
CD 1点
DE 2点
EF 1点
FA 1点
BX 1点
XD 1点
(2)連続する文字列長xの間で、連続する2文字のハッシュが合計何回でてくるかカウント（合計はしゃくとり法で求めました）
ABCDE 2+1+1+2=6点
BCDEF 1+1+2+1=5点
CDEFA 1+2+1+1=5点
DEFAB 2+1+1+1=5点
EFABX 1+1+1+1=5点
FABXD 1+1+1+1=5点
ABXDE 1+1+1+1=5点
(3)最高得点のやつが、もっともよく出てくる似た文字列。（ただこの得点のつけ方だと長い文字列が必ず有利になるので、得点のつけ方は、若干調整してます。）
この場合、ABCDEが6点で最高。

これを深さ優先探索（←全然ダメ）でやりました。枝の数は、Sの数に応じて、調整しました。

トップダウンで、長い単語から、平文から数字に置き換えていく。（最終的に企画倒れ）

今回、問題が途中で変更になり、error値が大幅に大きくなりました。そこで、平文がerrorによりぐちゃぐちゃになっても、まだ残っている情報ってなんだろう？「実は長い平文のほうが、残っている情報が多いから、復元のチャンスがあるのでは？」と思い、やってみたのですが…

まず、同じ文字の間隔が多いところを探す

同じ文字の間隔を使えないか？
ABCDEFABXDE
A-A 文字の間隔 4
B-B 文字の間隔 4
D-D 文字の間隔 4
E-E 文字の間隔 4

よく出てくる単語は、同じ間隔がでてくる回数も多くなります。文字間隔が小さいと（特に26以下）役に立たないけど（鳩の巣原理）、文字間隔が大きいときは、実際の文字間隔だけが突出した値になります。平文が長ければ多ければ、誤差が大きくても正しい単語間隔が見つかりました。

文字間隔から、実際の単語S[]の位置を探す

文字間隔dが既知となりました。文字間隔をdとしたとき、位置aと位置a+dが同じ文字になる場所を羅列します。横軸を単に順番のID（aの小さい順）、縦軸をaとしたとき、以下のようなグラフになります。

（エクセルシートのA列が、縦軸のaです）
このグラフを見ると傾きが平らな部分と、急でガタガタな部分にはっきりと分かれます。この平らな部分が実際単語がある部分、急な部分はたまたま同じ文字が現れた部分になります。というわけで、急な部文と平らな部分の境界が単語のスタート位置になるのが分かりますが、ここで問題がありました。

単語の位置は少しでもずれて置き換えてしまうと、その後の結果がひどいことになる。
意外と平らな部分とガタガタな部分の境界を正しく求めるのが難しい（１階微分・２階微分いろいろ試しました。）

というわけでトップダウンの方法は諦めました。ただ、この平らな部分の傾きからerrorを求めることができるので、それは副産物として使用しました。

個人用メモ

■ファーストインプレッションとその結果

- 基本的には、dataの生成方法をヒントにすると、かなり簡単にできるかもしれない。
  - （結果）その通りだが、生成方法をちゃんと理解してなかった。
- 見本のなかのerrorは予想できるのでは？
  - （結果）できた。そこそこ役にたった。
- 必ずしも、見本どおりの圧縮をする必要はない。再現が高いほうが重要。
  - （結果）神頼みフェーズで使ったが、甘かった…
- 必ずしも、圧縮文字列をすべて使う必要はない。短くてもOK
  - （結果）ぴったりじゃないと大体ダメなので…
- トップダウン/ボトムアップ/両側探索それぞれメリットありそう。ケースによってかえれるので、１つにこだわる必要はない。
  - （結果）結局ボトムアップと神頼みだけになった。
- トップダウンのときは、文字列の長さの予想が難しい
  - （結果）いろいろ試したが断念
- いろんな区間長で調べる必要があるかも。
  - （結果）？？？。何ですか？？
- エラーの予想は、ボトムアップの１段階目でできないか？
  - （結果）できた。これでもまぁまぁの結果だった。
- 答えSの読みこみ、Sの登場文字列数との比較はすごい重要な気がする。
  - （結果）やった。問題のinputでない値も、結果の比較用に積極的に使おう。

■キーワード（調べ物するとき用）
似た文字列は似たハッシュ値になってれば分類できる？

- 近似近傍点探索手法 Locality Sensitive Hashing(LSH)
- k近傍法
- kd木
- Metric tree
- ハッシュ
- continuos
- Locality sensitive hashing (LSH)
- 類似文字列検索アルゴリズム
- Divide Skip
- ハミング距離
- 宇野毅明

2014-03-01

TCO11 Round 2

TopCoder マラソンマッチ

(2011年6月29日の記事を移行したものです。)

結果

136位/222 Rating 1795→1694

このRoundで敗退かつレーティング的にも大敗北…

問題

複数の点がだいたいランダムに配置されている（点の数は50～5000）。それらの点を結んで多角形を作れ。

入力パラメータsidesDiff。1≦sidesDiff≦20。sidesDiffは多角形の各辺の、最小の長さと最長の長さの割合、もしsidesDiffが20だったら、最小の辺の長さは、最長の辺の長さの100-20=80%以上でないといけない。
入力パラメータradiiDiff。1≦radiiDiff≦20。radiiDiffはは多角形の中心（点の座標の平均）から、各頂点からの距離の、最小の長さと最長の長さの割合。sidesDiffと同様。
同じ点を２回以上使ってはいけない。
n角形につきn*n点もらえる。

点が少ないケース(Example1)

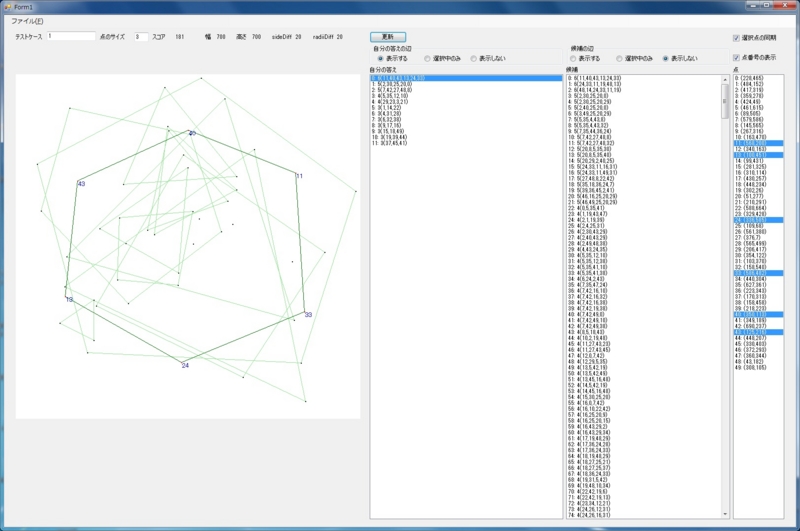
点が多いケース(Example7200)

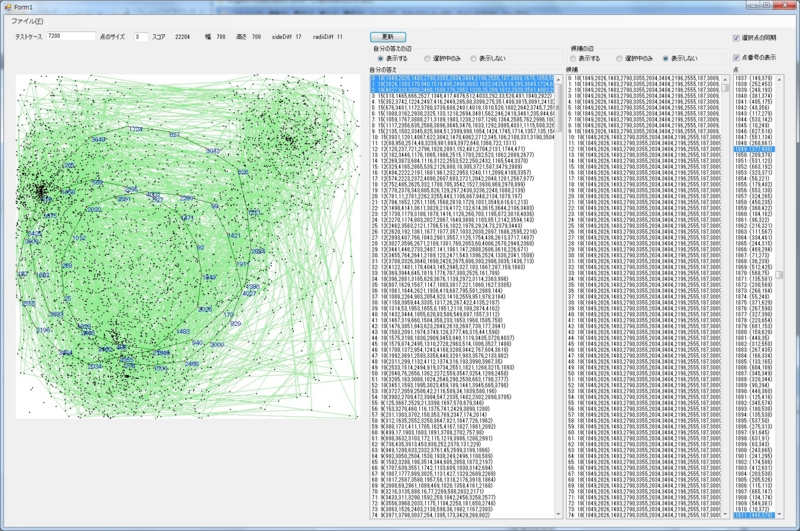
このように、つくるべき多角形は正多角形に近い形になります。

方針

今回は反省点が多いのですが、まずは、良さげ見える（が実は良くない）今回の目標と方針を書きます。あとで、失敗した点を書きます。

目標

今までのマラソンマッチでは、最高点が伸びなそうなアルゴリズムだったので、中途半端な順位だった→
「今回はすぐに結果がでないくてもいいから、到達最高点が伸びるような、計算量もギリギリまで使い切るような、スケールの大きいアルゴリズムにする。」

方針が決まるまでの流れ

「たいていの人は頂点数Nが多いときに苦戦するであろう」
→「計算量がNにあまり依存しないアルゴリズムを考えれば勝てるのではないか？」
→「下記のアルゴリズムなら、O(中央の点の数*N)と、Nのオーダーは1乗。しかも、計算量も中央の点を(1,1)おきにとれば、700*700*5000=2450000000で10秒ギリギリぐらい？いけるかも」
→「しかも、この方針は、正10角形を求めるのも、正100角形を求めるのも、かかる時間はそれほど変わらないので、めっちゃ有利」
実際以下の方針を思いつくまでに、10日ぐらい消費してしまいました…

方針

１．まず、中央の点(cx,cy)を決めます。

２．N個の点を極座標に配置します。各点のr,θを求めるのは三角関数で簡単に求まります。

３．座標に分けたので、θ方向に等間隔の座標にあれば、正多角形に近い形になります。

４．結局は、r,θの２次元の座標に落とせるので、「もし、ある(dr,dθ)の範囲内に点があるか調べたい」ときはDPを使えます。

だいたい、「θの範囲、rの範囲がどれぐらいに収まっていれば、正多角形ができるか？」についての基準は、あらかじめ別なプログラムで、sidesDiffとradiiDiffごとに求めておきました（ある半径rのn角形の,範囲dr・dθに点をランダムに配置し、sidesDiffとradiiDiffを満たす多角形ができるか調べる）。実際にこの部分の精度については、かなり高かったので、うまくいってたと思われます。

反省点

目標が間違ってる

そもそも「計算量をギリギリまで使ったアルゴリズム」が高得点とは限りません。欲しいのはスコアです。大きく勘違いしてます。

スコア分析がだめ！

これ、すごく重要で、初回のマラソンでは出来てたのですが・・・。この問題を「正ｎ角形で、できるだけｎが大きい多角形をたくさん作ろう！」と考えているようではダメです。もうちょっと細かくみていかないといけません。例えば、６角形１個は３６点、３角形４個も３６点です。大きい多角形を無理してつくるよりは、多くの小さい多角形をつくったほうが良い場合も十分考えられますよね。スコアについて、ほんとによく考えたほうがいいです。

計算時間あたり・頂点数あたりなど、単位を意識した考察ができていない。

６角形１個つくるのに1秒、３角形１個つくるのに0.1秒だったら、断然３角形をつくったほうが、時間あたりの得点が高いです。同じように、頂点数あたりの得点なんかも考慮するべきでした。今回の自分のアルゴリズムでは、計算時間あたりの得点について全く考慮していません。単位を統一して考えるのは、アルゴリズム以前の重要な問題です。これがちゃんとしてないと、そもそもアルゴリズムの良し悪しの比較ができなくなってしまいます。仕事では、めっちゃ注意しているのですが(T T)

「頂点数Nに依存しにくいアルゴリズム」にする必要はない。

別にNによってアルゴリズムを変えるのは全然構いません。Nに依存しないアルゴリズムは、裏をかえせば「Nが小さいときの有利さを生かせない」アルゴリズムでもあります。（ただ、複数のアルゴリズムを用意するのは、実装の時間はかかるので、１つに統一するメリットもあります。）

実装時間も考えて計画をたてよう。

誰でも思いつくようなケースをほとんど試さなかった。

特に、時間がかからずに実装できるものは、絶対試したほうがいいです。仮に全然結果がでなかったとしても、その後のヒントになる可能性もありますし、条件によっては使えるかもしれません。今回、自分の考えたのは実装時間がかかるため、それが外れ方針なのに気づくのに時間がかかってしまいました。

このアルゴリズムの欠点

実は、計算量が多くなり、(cx,cy)を調べられる箇所が少ない。

当初の予定では700*700マス（中央がマス上にあるとは限りませんが）調べる予定でしたが、だいたい10000～100000点ぐらいしか調べられませんでした。実は、
(1)r,θを等間隔で細かくとった場合（dr=1,dθ=1）、矩形でO(1)を計算するため、DPで2次元部分和を計算するときが計算量がO(rの分割数(=350)*θの分割数(=360))となり、頂点数Nより大きくなり、そこがボトルネックとなる
(2)r,θを等間隔ではなく、n角形時のdr,dθにあわせてとると、ボトルネックは解消されるが、n角形ごとに計算しなければならない。
最終的には(2)の方針でいきましたが、計算量的にはきつく、多くの(cx,cy)を調べることはできませんでした。

(cx,cy)の位置についての工夫がない。

全く思いつきませんでしたが、多くの人は中央を先に決めるという手法を使ってました。

「(cx,cy)を変えるたびに、N点配置する」ということ自体が損

もし(cx,cy)によらずに、再利用できるデータがあれば、それでも高速化できたはずです。

まぁ、いろいろ試して失敗した点（ひどい焼きなまし法とか）や、反省点（10秒に間に合ってないケースが5つあった）とかは、まだまだありますが、これぐらいで。

2014-03-01

TCO11 Round 1

TopCoder マラソンマッチ

(2011年6月1日の記事を移行したものです。)

結果

62位/368 Rating 1754→1795

大反省点

調査してね（インターネットつかえます）
文字を置く・何か置く、やり直し(Undo)が可能な部分については、最初からやり直し可能な実装をしていかないと、だめです。
最初の解答ができるまで、とにかく、がんばれ。
前回の反省点を守ろう。同じ失敗をくりかえす自分は最悪です(>_<)
マラソン開始日前に、もやもや要素をすべてとりのぞく。何も用事がない・借りがない状態でマラソンをスタートしましょう！
マラソン期間中に、アクシデントにまきこまれない。普通の生活をしよう。
Javaを自分の場合つかわないので、Javaでの採点部分や、scan部分などは、できるだけはやくC++に移植する。
ちゃんとマラソンスタートしたら、はじめる。毎日安定してやる。
はやめにスタートしたほうが、計算リソースを有効に使える。
- ぎりぎりなってからだと常にパソコンでプログラムを書きたいので、計算結果待ちとかの時間が無駄。はやいうちにスタートしておけば、夜中に計算とか、出勤中に計算とか、有効に計算リソースを使うことができる。
パソコン２台あるのを有効に使う

ポイント

（いろいろあったのですが、マラソンRound2前に書く時間がなくなってしまったので、すごいてきとーです・・・。せめてツールの画像だけでも。本当は画面右側に文字情報のリストが表示され、選択中のものだけ色を変えたりすることもできます。）

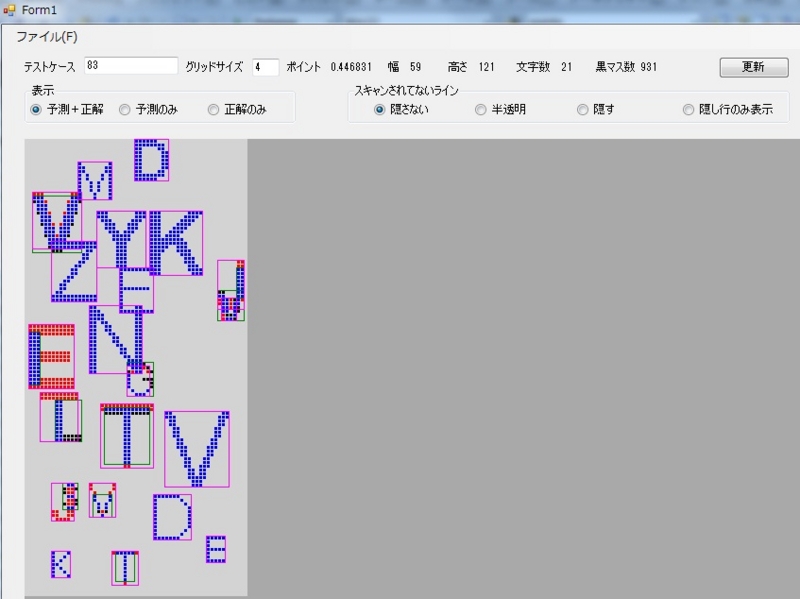
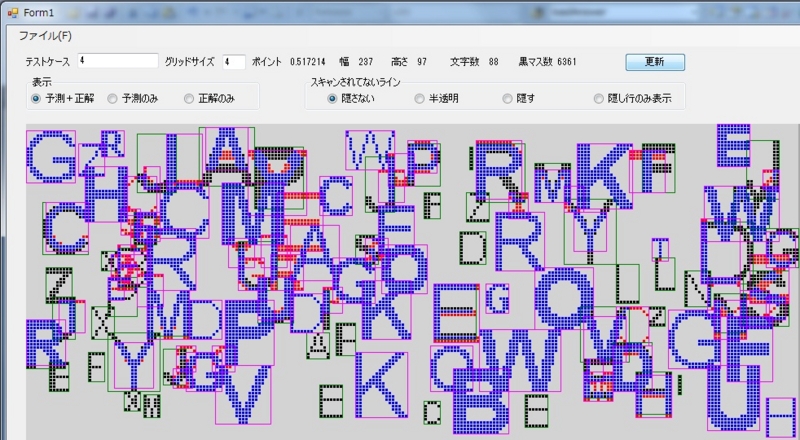
基本的には重なる黒のマスが多い文字からおいていったのだが、上のIのように、TLEはIに負けたりする。つまり、
「実際にはかなり合ってるのに、登場することができない不幸な文字があるのでは？」
と思い

外れている文字を使ったら選ばれにくくする
答えにあるのに使わない文字があったら選ばれやすくする

というのを多くのテストケースでまわし、文字の選ばれやすさの重み付けを決めるという方針で行った。
しかし、結果はほぼ効果がなかった。実際には、ほとんどの文字の「当たっているのに選ばれない」＝「当たっていないのに選ばれる」の確率はITLEなどを除き、ほぼ一緒になってしまった。