TCO11 Round 2 - じじいのプログラミング

(2011年6月29日の記事を移行したものです。)

結果

136位/222 Rating 1795→1694

このRoundで敗退かつレーティング的にも大敗北…

問題

複数の点がだいたいランダムに配置されている（点の数は50～5000）。それらの点を結んで多角形を作れ。

入力パラメータsidesDiff。1≦sidesDiff≦20。sidesDiffは多角形の各辺の、最小の長さと最長の長さの割合、もしsidesDiffが20だったら、最小の辺の長さは、最長の辺の長さの100-20=80%以上でないといけない。
入力パラメータradiiDiff。1≦radiiDiff≦20。radiiDiffはは多角形の中心（点の座標の平均）から、各頂点からの距離の、最小の長さと最長の長さの割合。sidesDiffと同様。
同じ点を２回以上使ってはいけない。
n角形につきn*n点もらえる。

点が少ないケース(Example1)

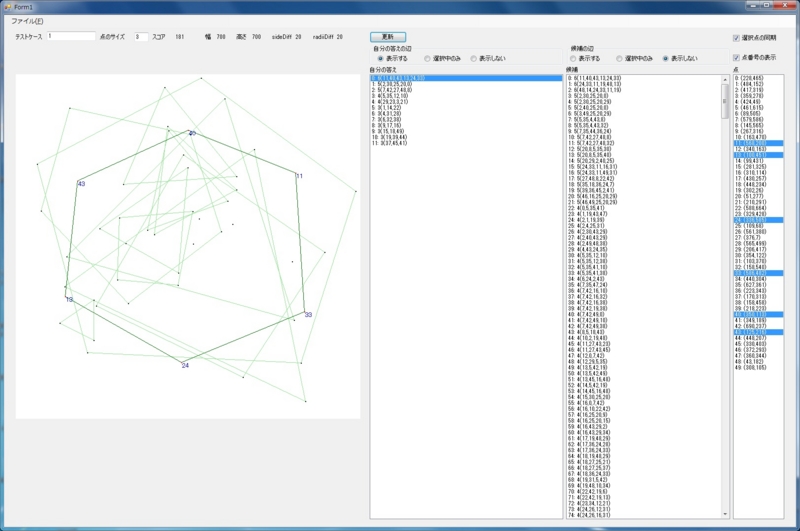
点が多いケース(Example7200)

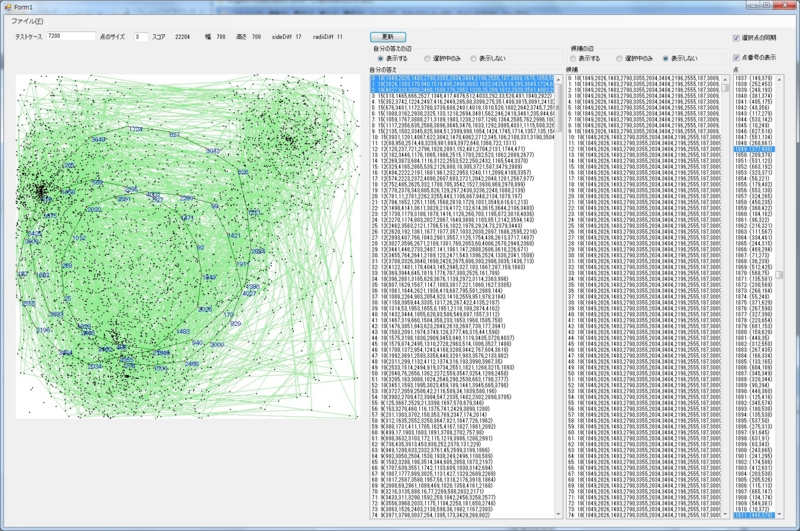
このように、つくるべき多角形は正多角形に近い形になります。

方針

今回は反省点が多いのですが、まずは、良さげ見える（が実は良くない）今回の目標と方針を書きます。あとで、失敗した点を書きます。

目標

今までのマラソンマッチでは、最高点が伸びなそうなアルゴリズムだったので、中途半端な順位だった→
「今回はすぐに結果がでないくてもいいから、到達最高点が伸びるような、計算量もギリギリまで使い切るような、スケールの大きいアルゴリズムにする。」

方針が決まるまでの流れ

「たいていの人は頂点数Nが多いときに苦戦するであろう」
→「計算量がNにあまり依存しないアルゴリズムを考えれば勝てるのではないか？」
→「下記のアルゴリズムなら、O(中央の点の数*N)と、Nのオーダーは1乗。しかも、計算量も中央の点を(1,1)おきにとれば、700*700*5000=2450000000で10秒ギリギリぐらい？いけるかも」
→「しかも、この方針は、正10角形を求めるのも、正100角形を求めるのも、かかる時間はそれほど変わらないので、めっちゃ有利」
実際以下の方針を思いつくまでに、10日ぐらい消費してしまいました…

方針

１．まず、中央の点(cx,cy)を決めます。

２．N個の点を極座標に配置します。各点のr,θを求めるのは三角関数で簡単に求まります。

３．座標に分けたので、θ方向に等間隔の座標にあれば、正多角形に近い形になります。

４．結局は、r,θの２次元の座標に落とせるので、「もし、ある(dr,dθ)の範囲内に点があるか調べたい」ときはDPを使えます。

だいたい、「θの範囲、rの範囲がどれぐらいに収まっていれば、正多角形ができるか？」についての基準は、あらかじめ別なプログラムで、sidesDiffとradiiDiffごとに求めておきました（ある半径rのn角形の,範囲dr・dθに点をランダムに配置し、sidesDiffとradiiDiffを満たす多角形ができるか調べる）。実際にこの部分の精度については、かなり高かったので、うまくいってたと思われます。

反省点

目標が間違ってる

そもそも「計算量をギリギリまで使ったアルゴリズム」が高得点とは限りません。欲しいのはスコアです。大きく勘違いしてます。

スコア分析がだめ！

これ、すごく重要で、初回のマラソンでは出来てたのですが・・・。この問題を「正ｎ角形で、できるだけｎが大きい多角形をたくさん作ろう！」と考えているようではダメです。もうちょっと細かくみていかないといけません。例えば、６角形１個は３６点、３角形４個も３６点です。大きい多角形を無理してつくるよりは、多くの小さい多角形をつくったほうが良い場合も十分考えられますよね。スコアについて、ほんとによく考えたほうがいいです。

計算時間あたり・頂点数あたりなど、単位を意識した考察ができていない。

６角形１個つくるのに1秒、３角形１個つくるのに0.1秒だったら、断然３角形をつくったほうが、時間あたりの得点が高いです。同じように、頂点数あたりの得点なんかも考慮するべきでした。今回の自分のアルゴリズムでは、計算時間あたりの得点について全く考慮していません。単位を統一して考えるのは、アルゴリズム以前の重要な問題です。これがちゃんとしてないと、そもそもアルゴリズムの良し悪しの比較ができなくなってしまいます。仕事では、めっちゃ注意しているのですが(T T)

「頂点数Nに依存しにくいアルゴリズム」にする必要はない。

別にNによってアルゴリズムを変えるのは全然構いません。Nに依存しないアルゴリズムは、裏をかえせば「Nが小さいときの有利さを生かせない」アルゴリズムでもあります。（ただ、複数のアルゴリズムを用意するのは、実装の時間はかかるので、１つに統一するメリットもあります。）

実装時間も考えて計画をたてよう。

誰でも思いつくようなケースをほとんど試さなかった。

特に、時間がかからずに実装できるものは、絶対試したほうがいいです。仮に全然結果がでなかったとしても、その後のヒントになる可能性もありますし、条件によっては使えるかもしれません。今回、自分の考えたのは実装時間がかかるため、それが外れ方針なのに気づくのに時間がかかってしまいました。

このアルゴリズムの欠点

実は、計算量が多くなり、(cx,cy)を調べられる箇所が少ない。

当初の予定では700*700マス（中央がマス上にあるとは限りませんが）調べる予定でしたが、だいたい10000～100000点ぐらいしか調べられませんでした。実は、
(1)r,θを等間隔で細かくとった場合（dr=1,dθ=1）、矩形でO(1)を計算するため、DPで2次元部分和を計算するときが計算量がO(rの分割数(=350)*θの分割数(=360))となり、頂点数Nより大きくなり、そこがボトルネックとなる
(2)r,θを等間隔ではなく、n角形時のdr,dθにあわせてとると、ボトルネックは解消されるが、n角形ごとに計算しなければならない。
最終的には(2)の方針でいきましたが、計算量的にはきつく、多くの(cx,cy)を調べることはできませんでした。