最小カットを使って「燃やす埋める」問題を解くスライドのフォロー

TopCoder

この記事は競技プログラマー向けです。

はじめに

以前、最小カットを使って「燃やす埋める」問題を解くというスライドを書きました。

www.slideshare.net

これに対して、tokoharuさんから、『燃やす埋める』よりも『Project Selection Problem』を使うべきという、提言がありました。
『燃やす埋める』と『ProjectSelectionProblem』 - とこはるのまとめ
続：『燃やす埋める』と『ProjectSelectionProblem』 - とこはるのまとめ

この記事は、それに対するフォローの記事です。

  • tokoharuさんの記事では、解法と問題名の双方について指摘されてると思いますが、この記事ではスライドの解法についての意見だけ書きます。（問題名については、twitterで別に考えを書きます。）
  • スライドに載っているのは、私の解法や解釈で、元の『燃やす埋める』の記事に載っていた解法とは違うので、ご注意ください。そちらに押しかけないように。
  • 「全部一緒でしょ」と思う人は、おそらく理解している人だと思うので、この記事を読む必要はないと思います。

解法について

解法の種類

主に以下の[A][B][C]のような解法があります。

[A] スライドの解法
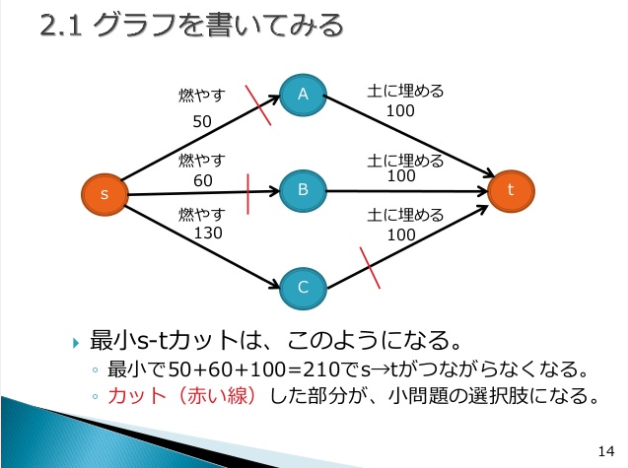
  • カットする辺が選択に対応します。小問題を並列に、選択肢を直列に並べます。
  • 最小カットになる辺の容量の合計が総コストになります。

スライドP14
f:id:shindannin:20171115014923p:plain

[B] プログラミングコンテストチャレンジブックの解法
  • カット後の頂点が、s側に属するか、t側に属するかで、選択を決めるという考え方です。
  • 最小カットになる辺の容量の合計が総コストになるのは[A]と同じです。
[C] Project Selection Problemのよく知られた解法

f:id:shindannin:20171115003256p:plain

[A][B]の本質はほぼ一緒ですが、分かりやすさについては、若干[A]が上回ると判断し、また[A]で対象の問題が全て解けたので、スライドでは[A]で統一しました。（当時、[C]は名前は知っていたのですが、誤解してました…。）

解法[A]のメリットとデメリット

[A]には以下のようなメリット・デメリットがあると思います。

【メリット1】定式化された最小カット問題と、直接結びつく。

最小カット問題を定式化すると以下のようになります。（Max-flow min-cut theorem - Wikipedia から引用です）
f:id:shindannin:20171115015238p:plain
辺(u,v)をカットする・しないを選択肢に対応させると、

  • d_{uv}=1のカットする辺が、「選択する」
  • d_{uv}=0のカットしない辺が、「選択しない」
  • 辺容量c_{uv}は、選択した場合にかかるコスト
  • 目的関数は \sum c_{uv}d_{uv}、かかるコストの総和、これを最小化する選択肢の組み合わせを探すということです。
  • 制約条件は、カットの条件で、小問題ごとに選択肢を１つ選ばなければならないのに対応しています。

最小カット問題とグラフが、特に変形などもせず、直接結びついています。これは以下のメリットにも、つながります。

【メリット2】選択肢の入れ替えをして良いというのが、分かりやすい。

選択肢の入れ替えは、制約条件が追加するにあたって、重要テクニックになってきます。スライドのP34～の内容です。その際、[B]のような解釈をすると、そもそも小問題ごとに選択肢を自由に入れ替えていいのか？という点で、少し迷うと思います（実際は可能です）。
f:id:shindannin:20171115024636p:plain

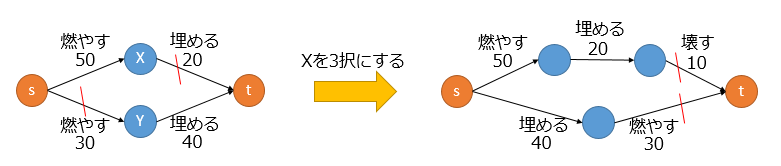
[A]の解釈であれば、（制約条件の辺を追加する前であれば）選択肢の順番が、最小カットに影響を与えないのは明らかです（どちらのケースでも、コストの最小値は20+30=50です）。
f:id:shindannin:20171115025114p:plain

【メリット3】3択以上でも適応可能というのが、分かりやすい。

[B][C]の解釈ですと、s側とt側の2つなので、3択には適応できないのでは？と、少し迷うと思います（実際は可能です）。
[A]の解釈であれば、3択以上に拡張しても問題ないというは、明らかです。（実際には、3択の場合、制約条件の追加が限定されて難しいのですが、それは、おそらく[A][B][C]どれも一緒だと思われます。）
f:id:shindannin:20171115025915p:plain

【デメリット】負辺の処理で間違える可能性が残る

tokoharuさんの指摘にあった、解法[A][B]のデメリット、負辺で間違う可能性がある（解法[C]では負辺がでてこない）ので間違えないということでした。それは正しいのですが、ただ、このスライドを読んだ人で、このP21が理解できず引っかかる人はあまりいないような気がします、自分はデメリットは些細だと思っています。
f:id:shindannin:20171114235119p:plain

また、[C]でも制約条件で負辺にあたるものが出てきた場合、どちらにしてもこの部分は理解してないといけない気がします。

評価

自分の考えでは、

  • 慣れた人にとっては、これらのメリットもデメリットも些細。
  • 慣れてない人にとっては、[A]がわかりやすい。

という印象です。
また、[A]と[C]は、「メモ化再帰」と「動的計画法」の関係みたいに、問題により若干有利不利はでてきますが、だいたいどちらでも解けるというかんじだと思います。複数の解釈を知っていたほうが、理解が深まることがあります。
さらに、[A]は、最小カットの式に素直に対応していて、一部にしか適応できない変なテクニックというかんじでもありません。

もちろん、[C]の解法は、もっと広まっていいと思うので、自分のスライドで出てきた問題をすべて[C]で解いてみる記事や、[A]と[C]で同じ問題を解いて比較する記事があればいいなぁと思っています。

おわりに

・念のためですが、この解法で解けるのは、最小カットの一部の問題のみです。一般性がすごくある解法と誤解せぬように。他の最小カットの問題も分類した記事があるとうれしいです。
・スライドは、自分の実力よりもだいぶ背伸びした内容になってます（この問題より、ずっと簡単な問題でも、解けてません…）。でも、気にせず記事を書きましょう。
→ぜひ、アドベントカレンダーへ（2枠目が過疎…）
adventar.org

2017/11/26 追記（特にためになったご意見です）

解法[B]のメリット（解法[A]のデメリット）

yosupotさん


tmaeharaさん


これらの問題では差がない。

southerwolfieさん